Write- up # 2

for

Jenni McIntire

Problem 10 in assignment 2

This problem investigates the graph of as the coefficients for the xy term change.

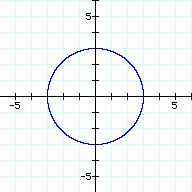
We first look at the case where the coefficient is 0. This produces the graph of a circle with the center at the origin and a radius of 3 units.

 

Now, on the same axis, we graph the general case where the coefficient is 1. By adding the xy term, this changes the graph from a circle to an ellipse.

 

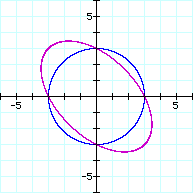
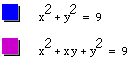
We next look at what happens as the coefficient changes. We look at the cases when it is 1, 0.5, and 1.5, in all of these the graph remains an ellipse, but the major axis changes. The larger the coefficient the longer the major axis. We also look at the cases when the same coefficients are negative. This rotates the ellipse 90 degrees, but the graphs are the same.

 

 

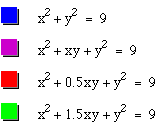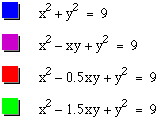It takes a different view when the coefficient is increased to 2.5, 3, 4,and 10. The graph is now a hyperbola. As the coefficient increases, the hyperbola becomes more curved. The same thing happens as above when the coefficients are negative( thethe hyperbola is rotated 90 degrees).

 

 

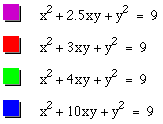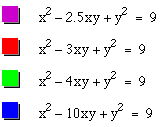When the coefficient is 2 or -2 the graph is two parallel lines. This can be justified by factoring into , then taking the square root of each side we get the two lines x + y = 3 and x + y = -3.

 

 

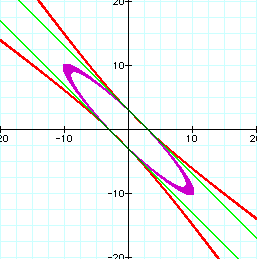
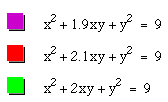
In conclusion, we can state that as the coefficient for the xy term is between 0 and 2 or 0 and -2 the graph will be an ellipse. When the coefficient is greater than 2 or less than -2 the graph will be a hyperbola. As the graph approaches 2 or -2 on either side, the graphs are becoming more linear.

 

Return