Write- up # 6

Given line segments j, k, m. If these are the medians of a triangle, construct the triangle.
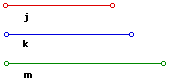
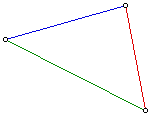
To start this construction, a triangle is constructed using the lengths of the medians given above.
Keeping the median m in place for the new tiangle, the centroid G is constructed since we know that the centroid is 2/3 the distance of the median from the vertex A. Then, two lines are construced through the centoid parallel to the sides. These lines will contain the corresponding medians of the new triangle.
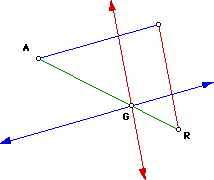
Again, we know the centroid is 2/3 the length of the median from the vertex, therefore we can construct two circles 2/3 the distance of the respected median from the centroid.
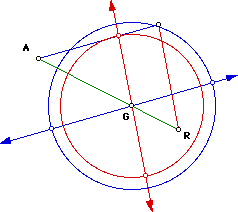
Since we know that A is one vertex, R must be the midpoint of the opposite side. Therefore, we must use the intersection points B aand C for the two other vertices.
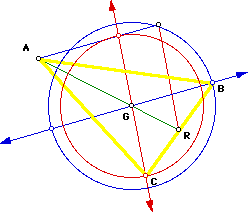
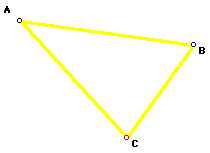
Triangle ABC should be the triangle with the medians j,k,m.
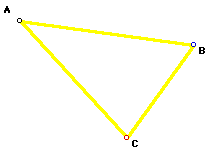
To test the triangle, we construct the medains of triangle ABC.
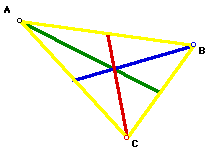
Then, three circles are constructed from the three vertices using the medians from above as the radii. Since the new medians are also the radii of rhe cirles, triangle ABC is the triangle with median length j,k,m.
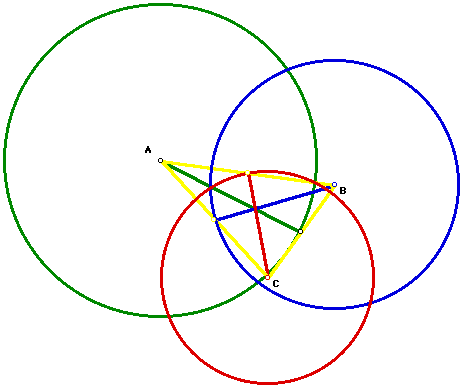
Solution:
Triangle ABC