

The triangles shown below are constructed from the triangle formed by points A, B, and C on circle O and circle O is the circumcircle of triangle ABC.
Triangle NKH, the red triangle, is the orthic triangle of triangle ABC. It is constructed by joining the feet of the altitudes of triangle ABC.
Triangle PMJ is constructed by connecting the points where the extended altitudes meet the circumcircle of triangle ABC. This triangle is shown in blue.
As you can see, the triangles look similar, but let's look further to see if they are and if so what other conclusions we might be able to draw.
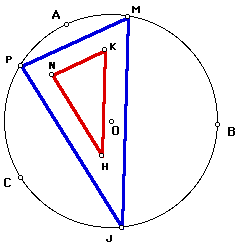
The following figure shows the lengths of the sides of the orthic triangle NKH and the triangle PMJ. Also shown are the angle measures of both triangles.
Notice that the angle measures are the same.
For triangles to be similar, the angles must be congruent and the sides must be proportional. As shown, the sides are in a 1:2 ratio.Therefore, the 2 triangles seen here are similar.
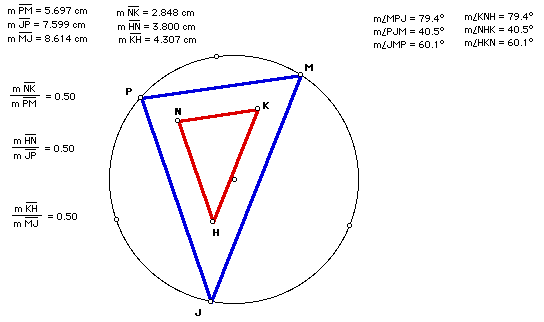
The figure below shows the triangles after they have been shifted and here they are still similar. Let's take a look at the triangles as they are moved to see if the similarity holds. Go to sketchpad and view for yourself. Follow the directions given.
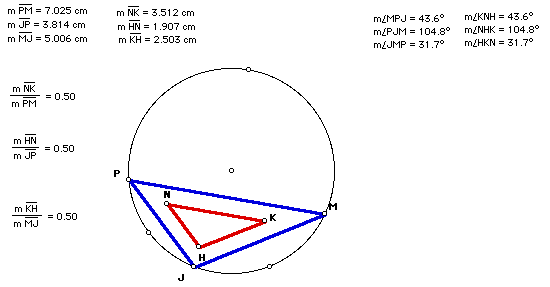
As the animation played, were there any times where the triangles did not hold their similarity?
What can you conclude about the orthic triangle and the triangle formed by the extensions of those altitudes to the circumcircle?