

The figure below shows the pedal triangle of point P. The pedal triangle is formed from the perpendiculars to the sides of triangle DEF from point P. The vertices of the pedal triangle, RST, are the points of intersection of the perpendiculars with the sides of the triangle.
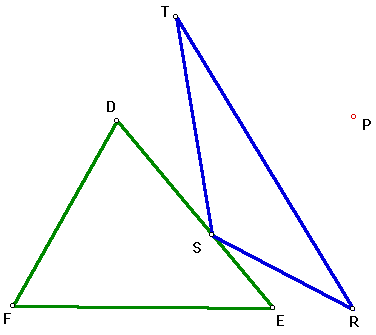
The following is a look at the aspects of the pedal triangle and its pedal point P with relevance to the circumcenter, orthocenter, incenter, and centroid of triangle DEF.
The following is a key for the letters given in the triangles:
C - circumcenter
H - orthocenter
I - incenter
G - centroid
P - pedal point
M1, M2, M3 - midpoints of the sides of triangle DEF
R, S, T - vertices of the pedal triangle
D, E, F - vertices of the original triangle
# 1 - C inside triangle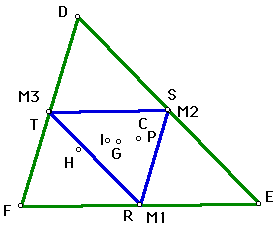 |
# 2 - C outside triangle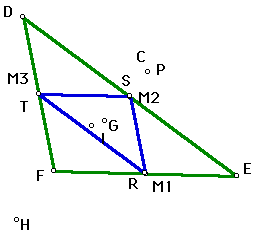 |
# 3 - C on side of triangle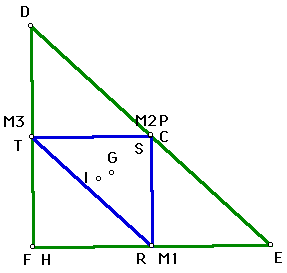 |
In the above figures, #'s 1, 2, and 3, when the pedal point P coincides with the circumcenter C, the pedal triangle, RST, has become the medial triangle of DEF. Remember the circumcenter is the point equidistant from the vertices of triangle DEF. Also the pedal triangle is formed from the perpendiculars from P to the sides of triangle DEF. Therefore, when the pedal point P is equidistant from the three vertices of triangle DEF, the midpoints of the sides of triangle DEF become the points where P is perpendicular to each side, thus coinciding with the midpoints of each side.
# 1 - H inside triangle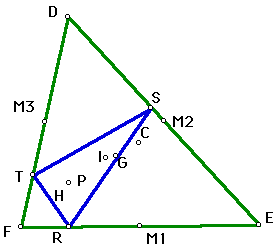 |
# 2 - H outside triangle |
# 3 - H on side of triangle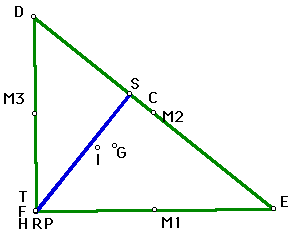 |
The above figures show the pedal point P coinciding with the orthocenter of triangle DEF.
As noted, in figure #1, the orthocenter is inside triangle DEF and the pedal triangle RST also remains on the interior of DEF.
When the orthocenter is on the exterior of triangle DEF, the pedal triangle also pulls to the outside of triangle DEF.
The orthocenter is the point of concurrency of the altiudes of triangle DEF. Since the pedal point P coincides with the orthocenter H, the vertices of triangle RST are in the direct line of the altitudes which form the orthocenter. In essence, this explains why the pedal triangle remains inside on the acute triangle (figure #1 above) and why part of the pedal triangle rests exterior (in figure #2 above).
Figure #3 shows the orthocenter on a side of triangle DEF, which is a right triangle. The orthocenter always coincides with the vertex of the right angle in a right triangle. Here where the pedal point P coincides with the orthocenter H, the pedal triangle becomes a straight line. This is called the Simson line and this occurs anytime the pedal point rests on the circumcircle of triangle DEF which vertex F is on the circumcircle.
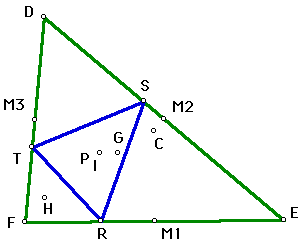 |
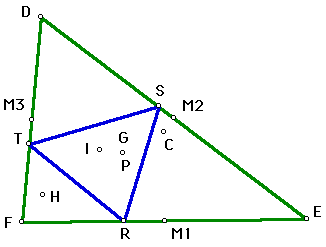 |
For both the incenter (I) and the Centroid (G), when the pedal point P coincides with those points, the pedal triangle will always remain on the interior of triangle DEF. Since the Incenter (I) is the point of concurrency of the angle bisectors and always remains in the interior of triangle DEF, then the pedal triangle will also stay interior. For the Centroid, the vertices of pedal triangle RST will remain on the sides of triangle DEF since it was constructed to the perpendiculars of the sides of triangle DEF. It should be clear that the pedal triangle would remain inside for the two above since the pedal point P is inside and is constructed from the perpendiculars to each side.