Final Assignment

for

Jenni McIntire

A. In triangle ABC, we select any point P inside the triangle and draw the lines AP, BP, and CP extended to their intersections with the opposite sides D, E and F respectively.

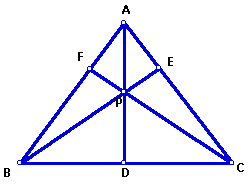
We eplore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

In the above triangle:

These products seemed to remain the same for all triangles no matter where P is located.

B. Conjecture: (AF)(BD)(EC) = (FB)(DC)(EA)

Proof: We start by constructing two lines parallel to AD through the the points B and C. Then we extend BE and CF to intersect the new lines at X anY respectively. This gives us similar triangles to work with.

C. We now look at the ratio of the area of triangle ABC to the area of triangle DEF.

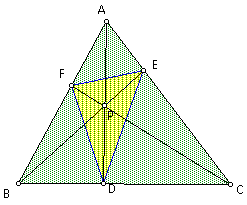
We can click here to see that the ratio of ABC to DEF is always greater or equal to 4.

This can be explained by the greatest area of DEF is when DEF is the medial triangle. When this occurs, ABC is cut into 4 congruent triangles, thus having a ratio of 4 to 1.

Return