

During the course of teaching the unit on circles in high school geometry, we came across something that was quite unusual and something that we were not aware of. As we know, a central angle and its intercepted arc have the same measure. We assumed that the only time an arc and its intercepted angle in a circle were equal was for central angles. As we began to teach the theorems on other interior angles of a circle an we came across the following.
The picture below shows the set-up of our problem.
Given a circle, say circle O, and two parallel segments, DE and BC for instance, construct a segment from D to C and from E to B. Also construct a central angle, DOE.
The problems were assigned to our students from a very similar set-up. The information that was given to them was that of arc DE and arc DB. Now, since the two segments, DE and BC are parallel the arcs DB and EC have the same measures. As our students worked on problems from the given, it seemed as though they were getting the angles DGB and EGC to equal the value of their respected intercepted arcs. As usual the students wanted to generalize and assume that these angles would always equal their intercepted arcs. Well as good Geometry teachers should do, we told our students that "no we should not assume this unless we know for sure or know a theorem that would back this up". The following picture displays an example of the problems' results.
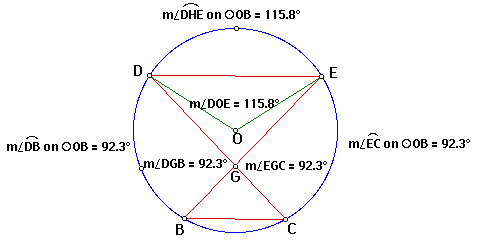
I have to say that I thought it kind of odd but did not think too long or hard about this. Then the next day , we assigned another set of problems that delt with the same set-up of the circle. As the students worked through the problems, guess what happened again? That's right. The angles and their intercepted arcs had the same value. Well I'm sure I looked thoroughly puzzled and I began to think through the central angle theorem. I have always assumed that this is the only angle in a circle that is equivalent to its intercepted arc. I began my to search my mind and to search books for a possible theorem to support this idea. I came across nothing. Jenni and I conversed about this and we could not come up with anything and went to another teacher who has taught Geometry for many years. She did not know of a theorem either. The next week in class, I asked Dr. Wilson if there was a theorem to support this and he also did not know of one.
To view the evidence of the above information click here to animate.
Maybe there should be a new theorem.
McIntire/Davis Theorem: Given that two chords of a circle, DE and BC, are parallel to each other in a circle, the angles formed by the intersection of DC and EB are equal to the measures of their intercepted arcs.
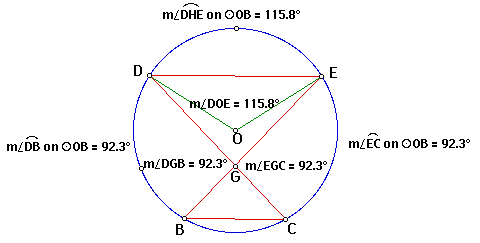
Proof: Since DE is parallel to BC, the measure of arc DB is congruent to the measure of arc EC. By the inscribed angle theroem, the measure of angle EBC equals half the measure of arc EC and the measure of angle DCB equals half the measure of arc DB. Therefore, since the measure of arc EC equals the measure of arc DB, by substitution measure of angle DCB equals the measure of angle EBC. Since the measures of each angle is equal and each angle equals half the arc, the sum of the two angles would be equivalent to the measure of the arc, DB or EC: by substitution, the measure of angle DCB plus the measure of angle EBC equals measure of arc EC and measure of angle DCB plus the measure of angle EBC equals measure of arc DB.
We also know by the exterior angle theorem of triangles that the measure of angle EBC plus measure of angle DCB equals measure of angle EGC and also equals measure of angle DGB. Therefore, by the transitive property of equality, measure of arc EC equals measure of angle EGC and measure arc DB equals measure angle DGB.
Thus an angle that is not a central angle of a circle is equal to its intercepted arc given parallel chords.