Write-Up #1: Explorations With Graphing Relations and Functions

Part 1: A Cursory Analysis of Variations of the Following Equation:

Given the following equations,

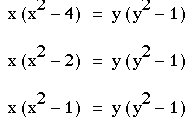
the graphs are superimposed on the same graph where the first equation is the red (burnt orange) line, the second equation is the purple line, and the third equation is the blue line.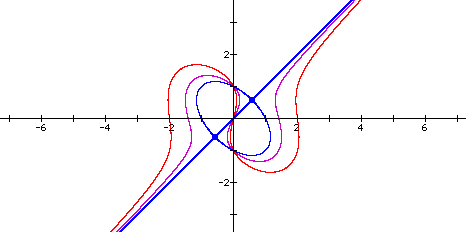

Essentially the lines are nested for various constants following the x-squared term with the exception of the constant one (1).

Part 2: Exploration of the General Sine Trigonometric Equation

We will investigate the following trigonometric equation

for the effects of different values of a, b, and c.

Investigation of the a-Value:

This value is the scalar constant of the trigonometric function which affects the amplitude of the function. Whatever value the sine function assumes, there is a multiplication by value a. The amplitude, which is the maximum and minimum attained values, will be the absolute value of a. If we observe the standard sine function where a=1, then the amplitude is also one. If the amplitude is changed, for example where a= 3 or 5, then the maximum and minimum values will be changed accordingly. Observe the graphs of three equations where a=1, 3, 5.

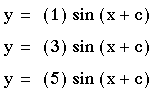
The first equation is in red, the second equation is in blue, and the third is in purple.

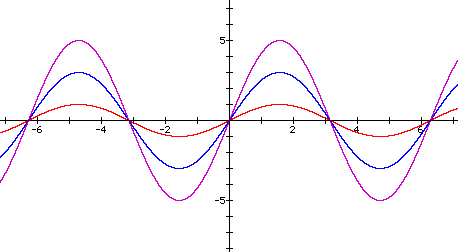
As is noted, the period is unaffected.

If a is positive, then the sine function, which has a zero value for a zero x-value and immediately assumes positive y-values within the first quarter of its period. If a is negative, then the sine function will immediately assume negative y-values within the first quarter of its period. These relationships can be graphically shown by the following equation where the blue line has an a-value of +5, and the purple line has an a-value of -5.

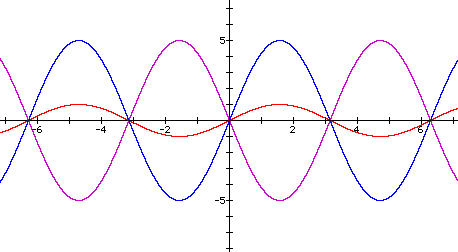
Again the period is unaffected.

Investigation of the b-Value:

This value is related to the period (T) by the equation of T = fundamental period / b where the fundamental period refers to the period of the trigonometric function being used (sine). Hence, there is an inverse relationship of b to the period. This relationship can be graphically shown by the following equations:

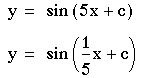
If we assume that c=o, and the standard graph is in red , the first equation has a b-value of 5 as shown in green. The period of this equation is now 1/5 the normal period of the sine curve. The second equation with a b-value of 1/5 , the curve shown in light-blue, now has a period of 5-times the normal period.

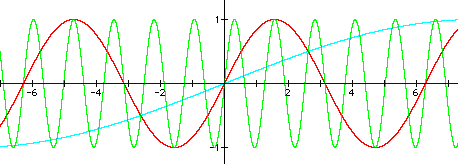
Investigation of the c-Value:

The c-values affect the starting point of the trigonometric function called the phase angle. The phase angle can be found by the equation x=-c/b. If we begin with an equation of y = a sin (ax + c), we can set a = 5 and b = 2, then we can investigate the different c-values.

For an investigation of different c-values, observe the following equations:

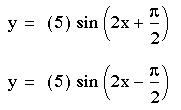
The first equation is in blue and has been shifted to the left from a starting value of x = 0 by -c/b, whereas the second equation is in purple and has been shifted to the right from a starting value of x = 0 by -(-c/b) = (c/b):

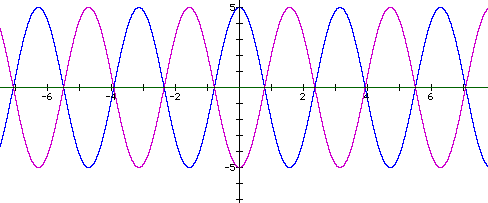
Hence the values of a, b, and c have very different impacts upon the graphs as has been illustrated, above.

RETURN to my Home Page