---

Write-Up #2: Exploration of the Quadratic Equation

This write-up investigates variations of the quadratic equation of

Part 1: Coefficient a

Although coefficient a can take on all real values from minus infinity to plus infinity, let us observe some positive values of 5, 2, -2 when b = 1 and c = 1. The equations are

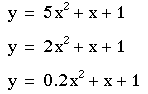
The first equation is graphed in purple, the second in red, and the third in blue.

There several conclusions that can be made:

(1) Since the coefficient is positive, the "arms" of the parabola open upward.

(2) All of the curves have a y-intercept of one.

(3) The largest distance between arms (third equation, graphed in blue) has a coefficient of .2, as compared to the smallest distance between arms (first equation, graphed in purple) has a coefficient of 5. Hence, the coefficient is inversely related to distance between arms.

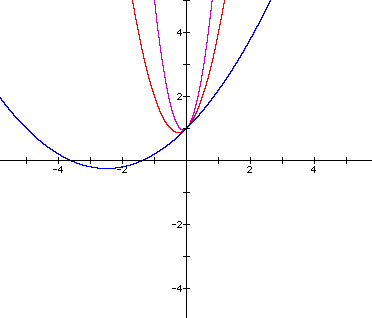
If the coefficient a of the squared term is negative, such as -5 and -2, then the graphs will open downward, will still pass through point (0,1), and will have the same proportions as the positive coefficients:

Lastly, if the a-coefficient, is 1 (the black line) or zero (the yellow line), then the graphs will still pass through point (0,1). The black line will appear as a "standard" (proportioned) parabola. The yellow line (with coefficient of zero) no longer has a squared term; hence, it merely represents a line.

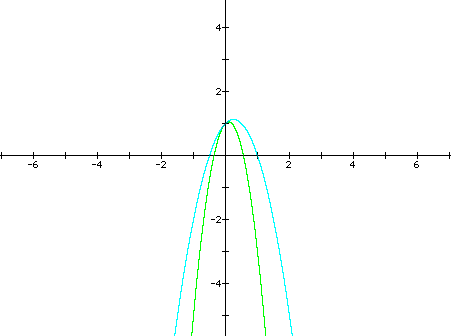
Part 2. Coefficient b

Coefficient b can also assume all real values. We will observe b-values of 5 (in purple), 3 (in red), 0 (in blue), -3 (in green), and 5 (in light blue). The positive values shift the curves in the opposite direction (left), and the negative values cause a shift to the right. All curves pass through point (0,1).

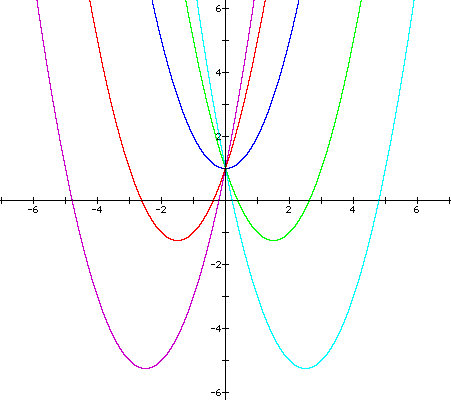
Part 3: Constant c

As a final investigation, we can now investigate the c-coefficient. This value can assume all real values, but we will investigate values of -3 < x < 3:

It can be noted that the c-variable corresponds to the y-intercept. For example, when c= -3, the y-intercept is at -3 (as illustrated by the purple curve), and when c= 1, the y-intercept is at 1 (as illustrated by the light-blue curve).

Part 4: Conclusion

The a, b, and c values have very specific purposes. The a-value serves to provide a scaling constant in an inverse relationship with the arms of the parabola and to open the arms up or down. The b-value serves to shift in the opposite direction of the sign of the coefficient. Finally, the c-value serves as the y-intercept in the same direction as the sign.