The Department of Mathematics Education

Write-Up #3:

Some Different Ways to Examine

by

James W. Wilson and Richard Moushegian
University of Georgia

General:

It has now become a rather standard exercise, with available technology, to construct graphs to consider the equation

and to overlay several graphs of

for different values of a, b, or c as the other two are held constant. From these graphs, we can observe the patterns for the roots of

For example, if we set

for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.

We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ( the point (0,1) with this equation). For b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will have two real roots, both positive). For b = -2, the parabola is tangent to the x-axis; hence, the original equation has one real and positive root at the point of tangency. For -2 < b < 2, the parabola does not intersect the x-axis; hence, the original equation has no real roots. Note that for b=0, the equation of the parabola has no linear term in x, and the graph of the parabola in centered on the y-intercept of (0,+1).

Similarly for b = 2, the parabola is tangent to the x-axis (one real negative root) and for b > 2, the parabola intersects the x-axis twice to show two negative real roots for each b.

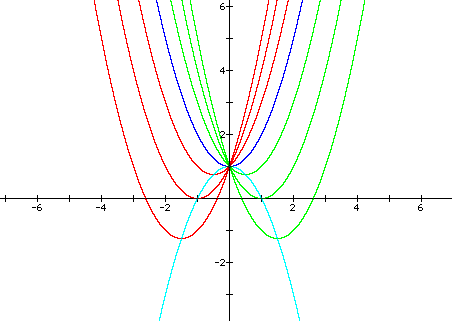
Now consider the locus of the vertices of the set of parabolas graphed from

.

where the curves with positive b-values are shown in red , negative b-values are shown in green, and the zero b-value is shown in blue.

The locus is a parabola which is shown as a light-blue curve with the following equation:

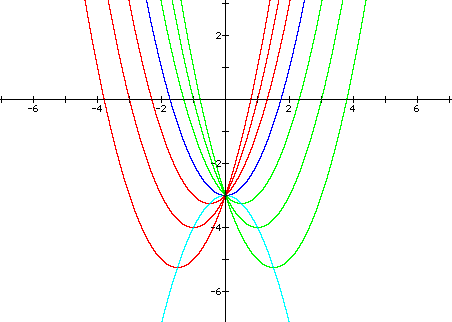
In general, the set of parabolas can be shifted along the y-axis by varying the constant, and the parabola passing through the vertices will also shift. This shifting can be shown with a different y-intercept as -3 with the associated graphs.

Graphs in the xb-Plane:

Consider again the equation

Now graph this relation in the xb-plane. We get the following graph.

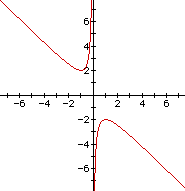
If we take any particular value of b, say b = 5, and overlay this equation on the graph, we add a line parallel to the x-axis. If it intersects the curve in the xb-plane, the intersection points correspond to the roots of the original equation for that value of b. We, therefore, have the following graph:

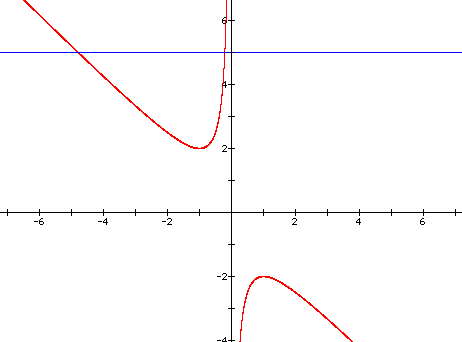
For each value of b we select, we get a horizontal line. Judging from the above graph, it is clear on a single graph what the roots are based on how the horizontal line intersects the hyperbola:

(1) If b > 2, there are two negative real roots for the original equation.

(2) If b = 2, there is one negative real root.

(3) If -2 < b < 2, there are no real roots.

(4) If b = -2, there is one positive real root.

(5) If b < -2, there are two positive real roots.

Suppose the conjecture is made that, half-way between the two points on either side of the b = 5 line, is the value (-b/2a) as part of the quadratic formula. Then the midpoint on the b = 5 line, in general, would be (-b/2a, 5). The slope of the line through the origin will be -2a/b. Hence, the equation of the line will be y = (-2a/b)x as illustrated by the following purple line:

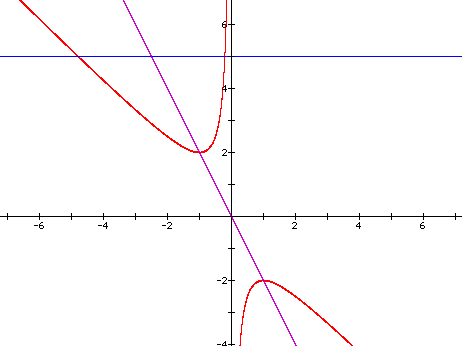
Also consider the case when c = - 1 besides c = + 1. Then we get a hyperbola that takes up the space on the other side of the asymptotes of the original hyperbola. Again the intersection points will be the roots of the equation.

Graphs in the xc-Plane:

In the following example the equation

is considered. If the equation is graphed in the xc plane, it is easy to see that the curve will be a parabola. For each value of c considered, its graph will be a line crossing the parabola in 0, 1, or 2 points -- the intersections being at the roots of the original equation at that value of c. In the graph, the graph of c = 1 is shown. The equation

will have two negative roots -- approximately -0.2 and -4.8.

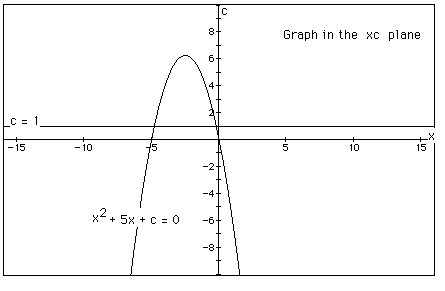
There is one value of c where the equation will have only 1 real root -- at c = 6.25. For c > 6.25 the equation will have no real roots and for c < 6.25 the equation will have two roots, both negative for 0 < c < 6.25, one negative and one 0 when c = 0 and one negative and one positive when c < 0.