

Write-Up #6: Observation of a Window
A 4 by 4 picture hangs on a wall such that its bottom edge is 2 feet above your eye level. How far back from the picture should you stand, directly in front of the picture (with observation angle BEA), or at some distance back x (with observation angle BDA)? Find the maximum viewing angle.
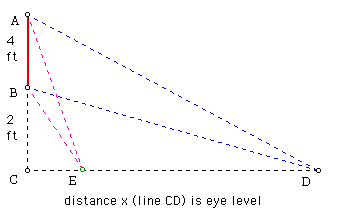
Labels:
Let angle ADB be a, angle BDC be b, and angle ADC be c.
Facts about the problem:
tan c = 6/x, tan b = 2/x, angle a = angles (c-b), and tan a = tan (c-b)
Recall: tan (A-B) = (tan A - tan B) / (1+tan A tan B)
Solution:
1. Using the above,well-known trigonometric identity and substituting the known relationships with unknown x,
tan a = tan (c-b) = (tan c - tan b) / (1 + tan c tan b)
= (6/x - 2/x) / (1 + (6/x)(2/x))
=
with an associated graph of
2. Using the subtilities of calculus, find the minimum value of the difference of angles: hence, take the first derivative of the above tangent function with respect to x, set it equal to zero, and solve for the unknown x. The value of x will be plus or minus two times the square root of three, or 3.464. (Ignore the negative value.)
3. Using the painstaking method of inverse trigonometric functions, we can find the angles:
a. Since tan c = 6/x or 1.732, then angle a is 60 degrees. (The range of the inverse function is -90 < a <90 degrees.)
b. Since tan b = 2/x or .5773672, angle b is 30 degrees.
c. Since angle a = c-b, then 60 - 30 = 30 degrees for angle a at an optimal distance (x) of 3.464 feet from the picture.
Generalization of the Problem:
Labels: Picture height is p and height above the eye level is h.
Facts about the problem:
tan c = (p+h)/x, tan b = h/x, angle a = angles (c-b).
Solution:
1. Substituting for the trigonometric identity using p and h,
tan a = tan (c-b) = (tan c - tan b) / (1 + tan c tan b)
which is equal to
divided by
or, simplified is equal to
.
2. Now we maximize angle a by taking the derivative of tan a, as before, but with the unknown quantities p and h. When setting the expression equal to zero and solving for x (ignore the negative square root quantity), we get
3. Hence, to find the angles,
a. angle c = arctan ((a+b) / x),
b. angle b = arctan (b/x), and
c. angle a = c - b = arctan ((a+b) / x) - arctan (b / x)
at distance x from the picture.
RETURN to my Home Page.