Write-Up #7: Tangent Circles

As Case I, if choose a small circle within a larger circle and a selected, arbitrary point along the larger circle, the problem is to construct and observe a tangent circle within the larger circle tangent at a point on the larger circle and tangent to the nearest point of the smaller circle.

To use the script, designate four points: the first is the small circle's center B, the second is point A for the radius BA of the smaller circle, the third is the larger circle's center D, and the fourth is point C for the radius DC of the larger circle. There will be an arbitrary point (shown as F) which is an arbitrary point on the circle. (If the circles are not constructed as shown below, then label the points and rearrange them.)

The construction will appear as follows:

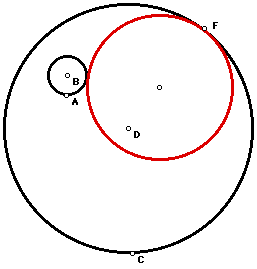
If we trace arbitrary point F about the larger circle (black) and observe the loci of the center of the tangent circle it will form an ellipse as shown in purple/blue. (Some of the construction lines are shown so that the loci of the center of the red circle can followed.)

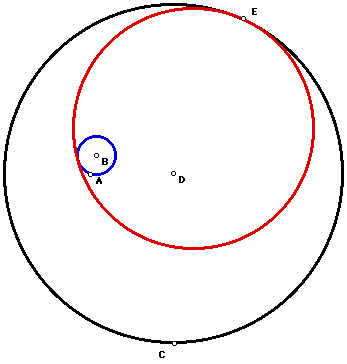
As Case II, we choose to draw a tangent circle (red circle) that is tangent to a large circle (black) at an arbitrary point E and inscribe the smaller circle (blue)(ie, tangent to the farthest point of the smaller circle), then the construction will be similar to the figure below.

To use the script, designate four points: the first is the small circle's center B, the second is point A for the radius BA of the smaller circle, the third is the larger circle's center D, and the fourth is point C for the radius DC of the larger circle. (There will be a point, shown as E, which is an arbitrary point on the circle.)

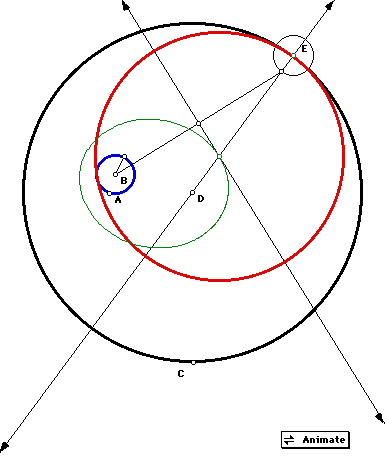
If we trace arbitrary point E about the larger circle (black) and observe the loci of the center of the tangent circle, it also forms an ellipse shown in green. (The construction lines are shown so that the loci of the center of the red circle can followed.)

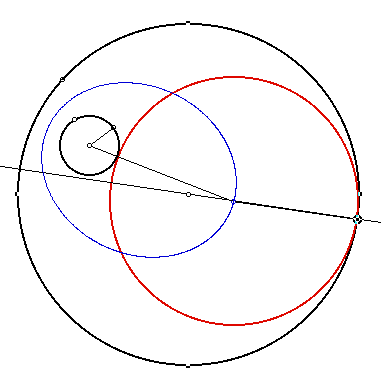
For some observations of different conditions, we will use Case I tangency requirements, but will overlap the two circles. The loci of the center of the tangent circle is an ellipse shown in purple.

If we continue to use Case I conditions, but separate the two circles, the loci of the tangent circle will be a hyperbola as shown below in purple.

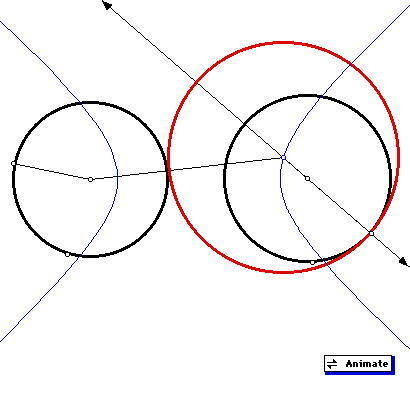
If we use Case II tangency requirements and overlap the circles, the loci of the tangent circle will be a straight line as shown in green. (There may be some inaccuracies in construction, but due to the nature of the construction, the loci has to be a straight line.) "It is intuitively obvious to the casual observer," to quote my physics professor when I was an undergraduate.

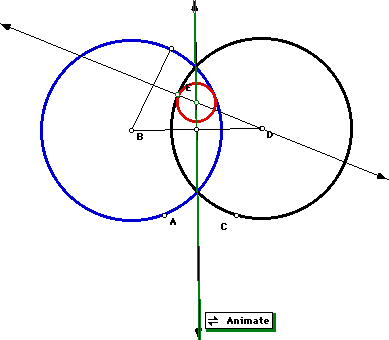
Finally, if we use Case II tangency requirements and separate the two circles, the loci of the tangent circle will be a hyperbola as shown in green.

The last construction will be obvious. It is based on the following figure which can be changed to the subsequent figure.

RETURN to my Home Page.