Write-Up #8: Investigation of Altitudes and Orthocenters

If we construct any triangle ABC, and find the orthocenter H, we can construct triangles with point H: BHC, AHB, and CHA. (Click HERE for the script.)

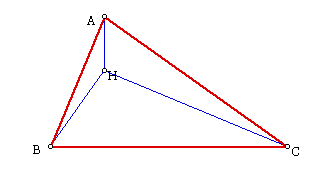
It becomes obvious, if we construct the orthocenters of each of these triangles (BHC, AHB, and CHA), that the vertices of the original triangle ABC are the orthocenters of the smaller triangles.

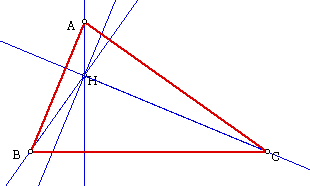
The rationale for this occurrence is due to construction of the orthocenter H. (See figure below.) Recall that H was determined by the intersections of the projections from Point A to the opposite side BC, from Point B to the opposite side, and the same for Point C. Hence, for triangle BHC, A is already the altitude of BHC. In order to construct the orthocenter H, an altitude was constructed with Point C to side AB, so Point A is also perpendicular to the extension of HC. A similar argument can be made for altitude from Point B to side AC so that Point A is also perpendicular to extension of BH. Hence, Point A is the orthocenter of triangle BHC. (A similar argument can be made for the other triangles involving Point H with respect to the vertices of the original (red) triangle.)

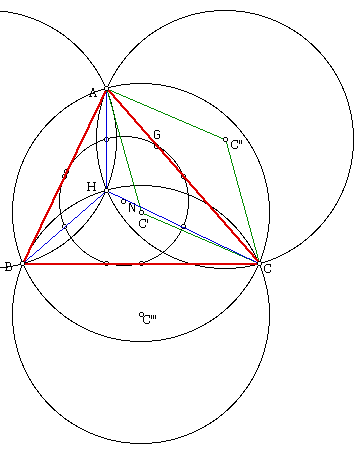
If we construct circumcircles for triangles ABC, AHB, BHC,CHA and a Nine-Point Circle for ABC, then the resulting figure will appear as below. (Click HERE for the script.)

Note that the circumcircles make for an interesting figure. Of particular note are two types of symmetry for further exploration in this write-up: (1) symmetry about the legs of the original ABC triangle (red), and (2) symmetry about the legs of the orthotriangles AHB, BHC, and CHA (blue).

Part 1. Symmetry About the Legs of the Original ABC Triangle

Note that the two circles through points AHC and ACB (see figure below) are reflected through line AC. This fact appears because the circumcircles C' and C'' were constructed through points A and C; hence, the circles C' and C'' have the same radii. The triangles ACC' and ACC'' are isosceles triangles with the same base. Hence the two circles have the same chord, the circles reflections of each other through the line AC, and the circles are congruent to each other. The same argument can be made about the other two sides of triangle ABC (red).

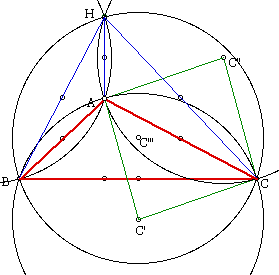
Part 2. Symmetry About the Legs of Orthotriangles AHB, BHC, CHA Observe the three pedals (black) inscribed inside the given triangle (red) radiating from Point H with the vein of the pedal in blue. Not only is it pleasing to the eye, but it obviously indicates some sort of symmetry. Note that for circumcircle through points AHC and ACB the circles are reflected through line AC and are congruent to each other. The rationale this relationship is true is a similar argument as was described above, but using common chord of HC.

Hence, we can conclude that all four circumcircles are congruent to each other.

We can also conclude that Point A can be interchanged with Point H because, as we mentioned before, the vertices of the original triangle ABC are the orthocenters of the smaller triangles (BHC, AHB, and CHA). If the interchange takes place we will have the same figure, except for the fact that the labels A and H are interchanged, and the shadow of the nine-point circle can be seen.

RETURN to my Home Page.