Write-Up #10:

A parametric curve in the plane is a pair of functions

x = f(t)

y = f(t)

where the two continuous functions define the ordered pairs (x,y). The two functions are normally called parametric equations of a curve, and the curve is dependent upon the range of t. We will be investigating parametric curves using trigonometric functions.

For a basic understanding of parametric equations, consider the following:

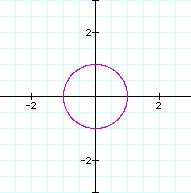
Since t varies from 0 to, the full domain of the functions, then the equations completely describe a circle. Note that the radius of the circle is one, which is the coefficient of the two equations.

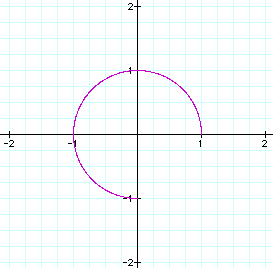
If t only varies 75% of the domain, then the described curve will only be 75% of a circle.

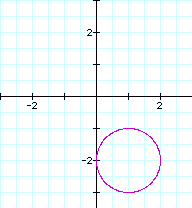
If we add constants to the parametric equations, such as

then the constants will translate the circle +1 unit in the x-direction and -2 units in the y-direction as follows:

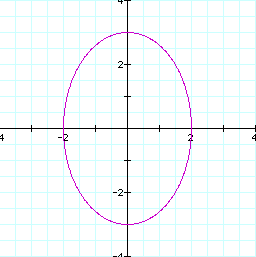
If we chose different coefficients for the two functions, such as

then the shape is altered, and it becomes an ellipse. The x-axis now becomes the minor axis with a distance of 2 units from the center (0,0), and the y-axis is now the major axis with a distance of 3 units from the center.

Hence, we can conclude the general parametric equations for our exploratory study are

where (m, n) is the center of the ellipse, 2A describes the length of the axis in the x-direction and 2B describes the length in the y-direction. These relationships can be graphically illustrated as (with the wonders of MacPaint)

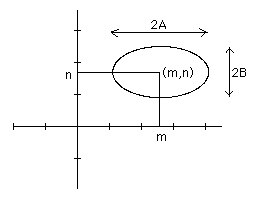
As an example of the above general equations, we have the following:

with the associated graph, below. Note that the center is (1,-2), the x-distance from the center to the right edge is 2 units (along the minor axis), and the y-distance from the center to the top edge is 3 units (along the major axis).

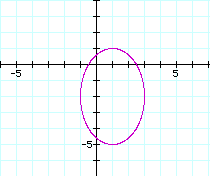
Now that we have covered the basics, we will investigate the following parametric equations where the basic function has a coefficient of two, and the function is raised to exponent n,

.

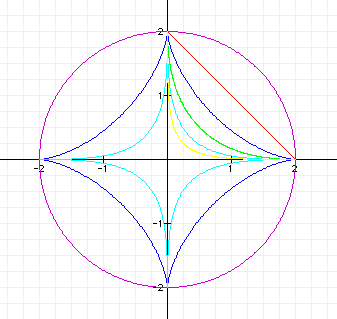
Then we obtain an unusual set of curves:

When n=1, the graph is a circle (purple) with radius 2, as expected.

When n=2, the graph is a (line) segment (red) in Quadrant I, inside the circle.

When n=3, the graph is a diamond (blue), inside the above line.

When n=4, the graph is an arc (green) in Quadrant I, inside the diamond.

When n=5, the graph is a smaller diamond (light blue), inside the larger diamond.

When n=6, the graph is an arc (yellow) in Quadrant I, inside the smaller diamond.

We can conclude that the even exponents produce a figure only in Quadrant I, whereas the odd exponents produce a symmetric figure that covers all four quadrants.

As another interesting variation, we can observe the graphs of

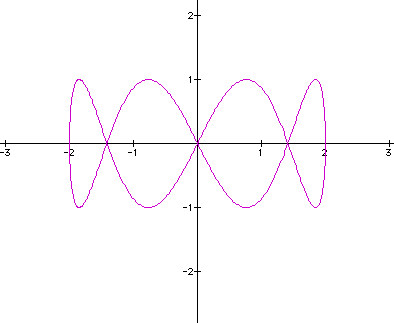
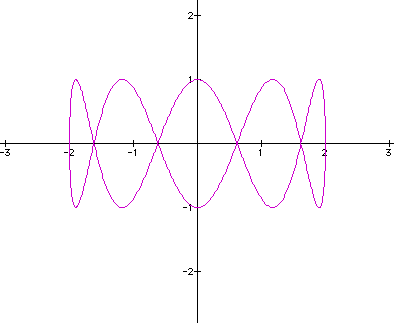
x = 2 cos (at)

y = sin (bt)

where a and b are integers. If a = 1 and b = 2, or greater, we note that b determines the number of loops. The boundaries of the loops lie between -2 and +2 along the x-axis, and -1 and +1 along the y-axis since the coefficients of cosine and sine are 2 and one, respectively. If b is even, the middle node is located at the origin.

Observe the two graphs when a is fixed at one, and b is 4 and 5, respectively.

RETURN to my Home Page..