

Write Up #11:
Part A: Basic Investigations of Polar Coordinates
Polar coordinates involve a pole and two rays, an initial ray, typically along the positive x-axis, and a terminal ray that sweeps counter-clockwise around a pole (the origin) and is measured by some angle theta, and is measured from the pole by a distance r (radius). The typical polar equation involves sine and cosine in the form
We wish to investigate the following curve
for various values of a, b, and multiples of theta.
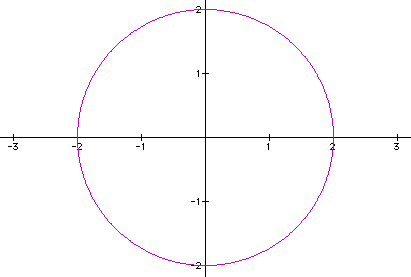
Case 1: For a=1, b=0, and theta = 0, the equation is the degenerate case of a circle about the origin:
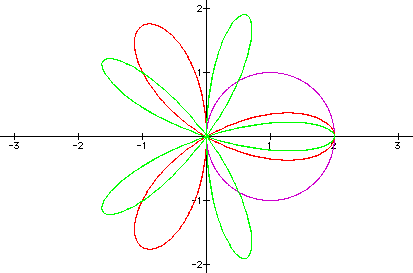
Case 2: For a=1, b=0, and odd, integer values of k, we get a "k-pedal" graph where the number of pedals is equal to the value of k: k = 1 yields one pedal (purple); k = 3 yields three pedals (red); and k = 5 yields five pedals (green). Note that since a is one, the coefficient of the sine function is 2 and the length of the pedals is two.
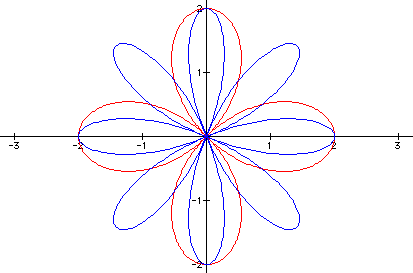
Case 3: For a=1, b=0, and even, integer values of k, we still get a "k-pedal" graph, but the number of pedals is twice the value of k: k = 2 yields four pedals (red); k = 4 yields eight pedals (blue); and k = 6 yields twelve pedals (not shown, because it is a mess).
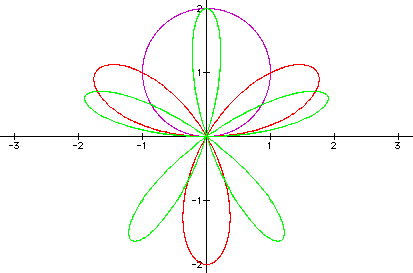
Case 4: For a=1, b=0, and using the sine function instead of cosine for odd values of n, we note the graphs are rotated:
Case 5: Returning to the cosine function for continued investigations, we investigate values of a (when b=0 and theta multiple k is five for 5-pedal figure), for values of 1, 2, and 3 of the following equation:
Notice that a is a multiplier of the figures as noted below:
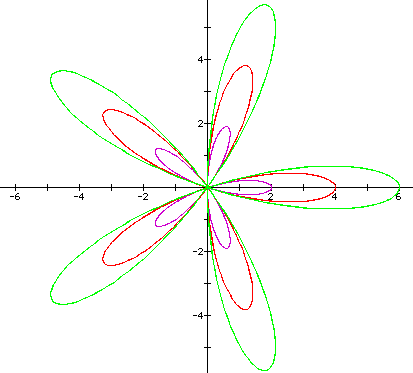
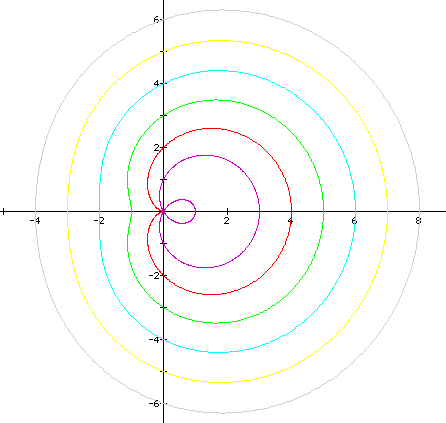
Case 6: Continuing with the same cosine function ,
we will hold a=1 and study b = 1, 2, 3, 4, 5 for various values of k. If k = 1, then we note that b < the coefficient of cosine, and the figure is a lemiscon (purple). If k = 2 (b = coefficient of cosine), then the figure is a cardioid (red). For k = 3, 4, 5, and higher (b > coefficient of cosine), then the cardioid figure looses its shape and approaches a circle as k increases (green, light-blue, yellow, respectively):
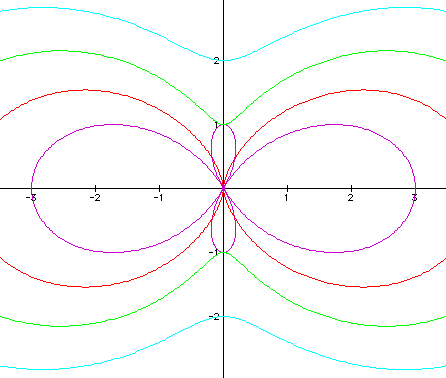
Case 7: With the same cosine function ,
we will hold a=1 and study b = 1, 2, 3, 4, 5 for k = 2, then we notice the same things happen, but the figures are different. With b < the coefficient of cosine, and the figure is a 4-pedal figure (purple). If k = 2 (b = coefficient of cosine), then the figure loses shape and only has 2 large pedals (red). For k = 3, 4, 5, and higher (b > coefficient of cosine), then the 2-pedals continue to lose shape, but increase in size as k increases (green and light-blue, respectively):
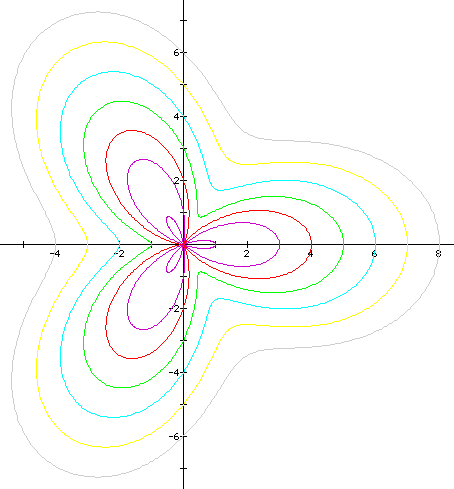
Case 8: Continuing with the same cosine function ,
we will hold a=1 and study b = 1, 2, 3, 4, 5 for k = 3, then we notice that the figures are different, but the same things happen. With b < the coefficient of cosine, and the figure is a 3-large pedal figure with an internal pedals (purple). If k = 2 (b = coefficient of cosine), then the figure loses its internal pedals (red). For k = 3, 4, 5, and higher (b > coefficient of cosine), then the pedals themselves continue to lose shape, but increase in size as k increases (green and light-blue, yellow, and gray, respectively):
Part B: An Interesting Form of Polar Coordinates
LINK HERE for Ken Hayakaya's investigation.
RETURN to my Home Page.