Essay #1: Exploration of the Gingerbread Man Using Excel
The purpose of this study is to
1. Illustrate recursive formulas
2. Illustrate the use of different seed numbers in recursive formulation
3. Illustrate the use of a spreadsheet analysis
4. Illustrate the use of graphing from charts
The given recursive formula in x and y for the purpose of this study is
x(n+1) = 1 - y(n) + |x(n)| and
y(n+1) = x(n).
Since the above formula is recursive (each successive value is dependent upon the prior value(s)), then we must select seed (initial or starting) values, (x(0),y(0)).
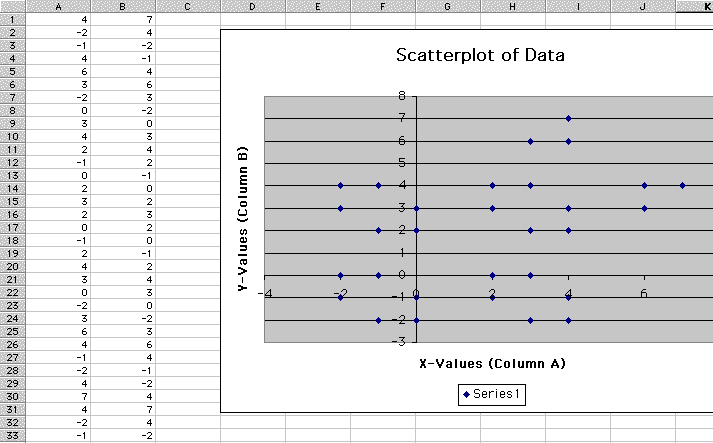
For example if the seed point (4,7) is chosen with 500 iterations of the formula, then we can construct a chart and a graph using Microsoft Excel Spread Sheet and their associated Charting Wizard. The chart below illustrates the first 33 iterations, but the following graph is plotted using the full 500 iterations. (Note: The X-Values are in Column A and the Y-Values are in Column B.)

The loci of dots appears to be a gingerbread
man in which the head is located at the lower left, the arms are
splayed out in a northwesterly and southeasterly directions, and
the two legs are are splayed out (the two cluster of three dots)
on the upper right corner. This example only produced 30 dots,
even though there were 500 iterations. Hence, we know that the
values must repeat themselves. Notice that the first three values
are repeated beginning with line 31. (Of course, the repeated
values are in the same order since they were generated by a
recursive formula.)
Approach:
Several numerical studies were conducted of seed points to determine if a better gingerbread man could be found. This study is based on 45 experiments with the associated charts and graphs.
First Approach and Results:
The first study selected different values of x: -6, -3, 0, 3, and 6. Then for each value of x, the y-values were varied as follows: -6, -3, 0, 3, and 6. Then each set of 500 iterations were plotted to see if we could get a better gingerbread man picture. The results varied widely.
Results: One result was that in certain cases there were so few dots that there was virtually no figure. For example, for seed values of (0,0) and (3,3), there were 6 and 5 dots respectively. See the next two figures with some of the data. Notice how the data repeats itself very quickly.
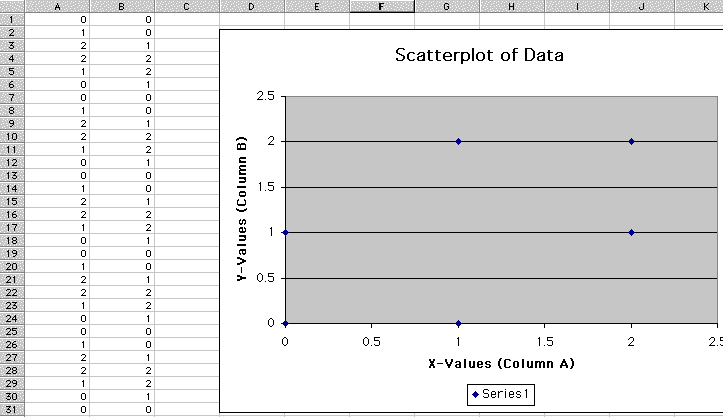
For example, notice in the following figure there are only 5 dots. The chart to its left shows how the data repeats itself after the fifth line.
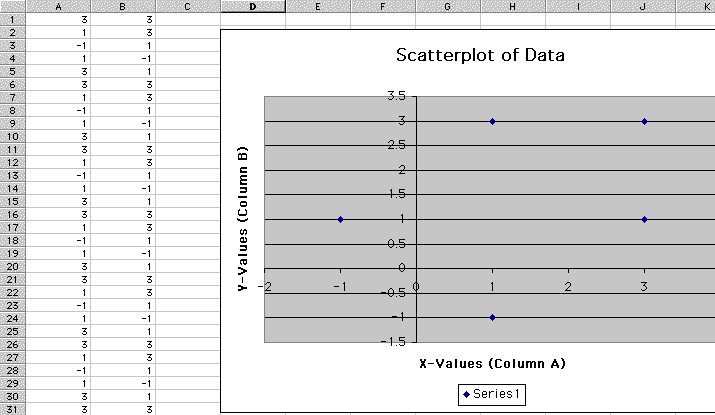
Other combinations resulted in some sort of border around a region. Seed point (-3,0) generated a single border of 24 dots, so the formula repeated itself after 24 iterations. (See the figure below.)
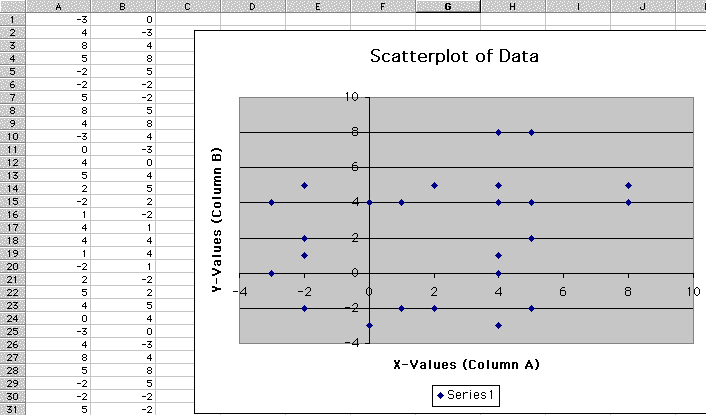
This border illustration could become very pronounced with groups of 6 dots defining a border. Note that seed value of (0,6) created a figure consisting of 96 dots in the figure below.
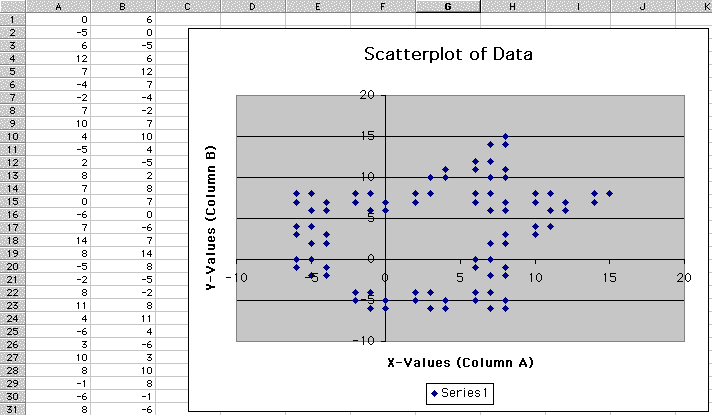
There were some decent gingerbread figures using some seed values of (0,3), (3,0), and (3,6). All three figures had 30 dots, so the formula repeated after 30 iterations. (See the next three figures.)
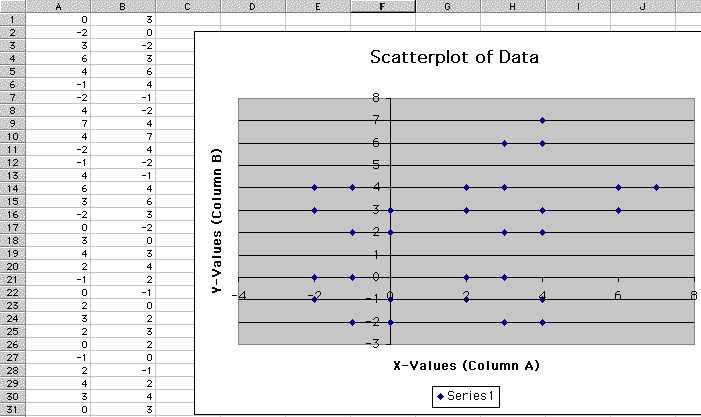
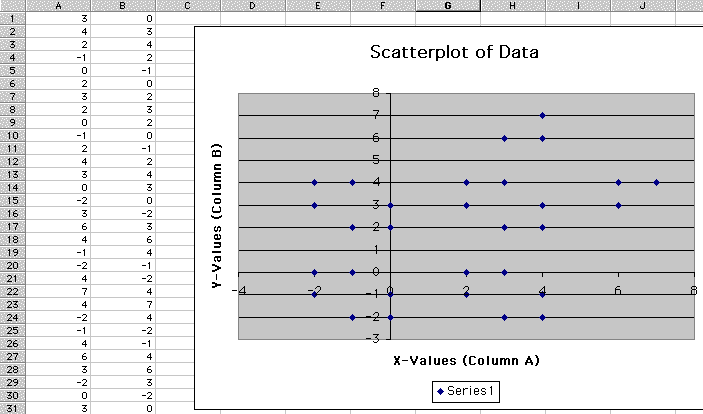
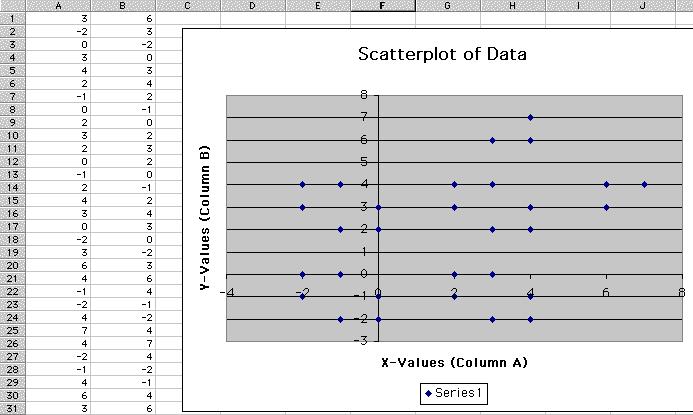
Second Approach and Result:
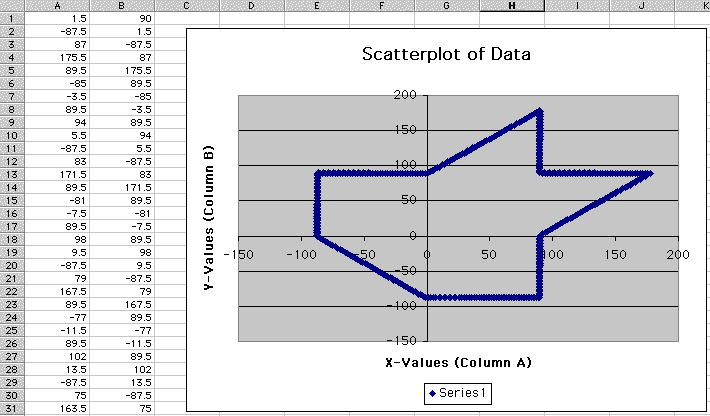
I then chose a reasonable starting value in x and a significantly large value in y. My seed value of choice was (1.5, 90) with the resulting figure. The pattern did not repeat itself after 500 iterations. Hence, it is a very dense figure.
Third Approach and Result:
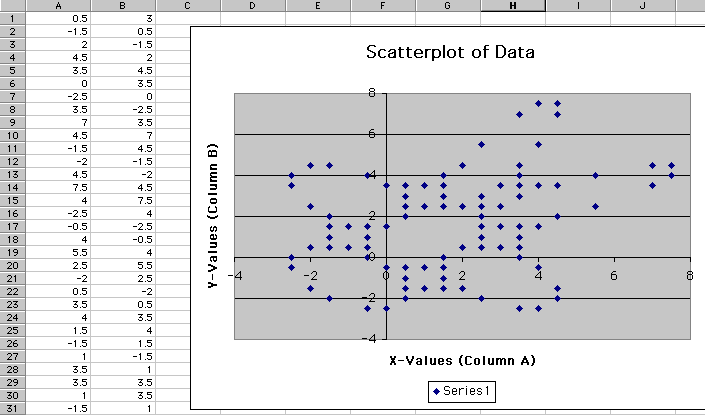
I chose different combinations to find a good gingerbread figure, but did not fin any consistent predictor. For example, I found (.5, 3) to be a good figure where the y-value was 6 times the x-value.
Although I tried (1,6), where y is 6 time s the x-value, the figure consisted of 33 points defining a single border around a region.
As a parenthetical remark, I found another
combination of (.25, 2) that resulted in a good figure, but the
(1, 12) resulted in a 79 data points defining a border around
a region using clusters of triple points.
Conclusions:
This study used recursive formulas, spreadsheet analysis, graphing analysis, and some statistical analysis to study seed point selection. The tools are excellent for illustration purposes, but unfortunately the particular recursive formula did not consistently produce good gingerbread figures.
My conclusions are that a student would either have to stumble upon some good seed combinations to produce good figures or conduct an exhaustive statistical analysis. Another conclusion is that this study taxed the memory of this machine.