Essay #3: Boxes Within Boxes and Triangles Within Triangles
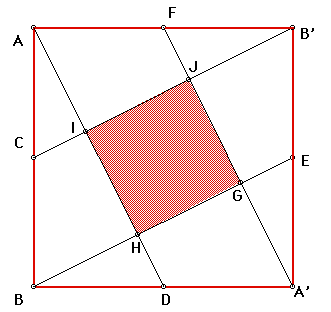
First construct a square (script: square).
Then connect each vertex to the midpoints of the opposite sides (script: midpoint-square). As shown in the following figure, the construction lines generate a square. It is this square that we wish to find the volume of the smaller red square in the middle in relation to the given square.

The ratio of the small, red square to the large red square can be found by algebra or geometry. However, we will use technology to determine the ratio as a visual proof in order to assist the student in visualizing the problem.
First, if we allow the computer to calculate the area of the small, interior box (GHIJ) over the area of the larger box (ABA'B'), the ratio is .20 (and its reciprocal is 5, meaning the larger box is 5 times the area of the smaller box).
Secondly, by using parallel construction lines,
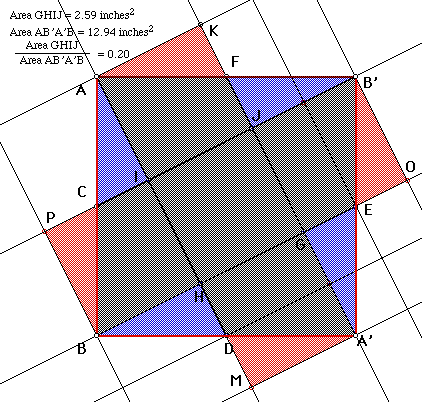
In a more general case, we can choose Point I along segment AB. With computerization (using Geometric Sketch Pad, GSP, program), we can calculate the inside square, the outside square, and their ratios depending upon the distance that Point I is located along segment AB from Point A (ie, a variable distance).
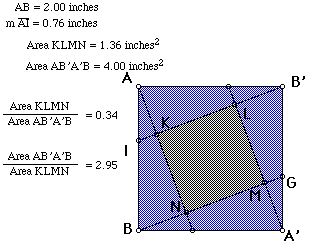
To further illustrate the relationship, an animation is available where the point follows a path along segment AB. (To activate this animation, CLICK HERE.)
As the animation will reveal two characteristics of this construction:
1. The closer Point I is to Point A, the larger Area KLMN is. In fact, it approaches Area AB'A'B.
2. The farther Point I is from Point A, the smaller Area KLMN is. In fact, it approaches zero.
As a further exploration in technology, let us look at the triangle ABC and construct an internal triangle using medians (lines from vertices to the midpoint of the opposite side), similar to what we did in the above square.

Obviously, when the medians are drawn, there is no internal triangle, since the medians meet at a common point called the centroid (See Points G, H, and I). (A similarly constructed triangle is available for personal exploration by using the following script.)
Now, if we move Point D along the line BC at variable distances from Point B (while the other points E and F are moving proportionally along their respective line segments), then we will obtain a triangle GHI within the original triangle ABC.
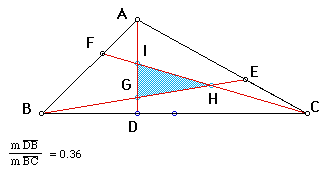
As a parenthetical remark, triangle GHI is not similar to triangle ABC since angle BAC is not congruent to angle GIH.
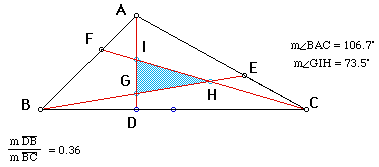
Now we can either manually move Point D along the segment BC or animate along the same path while while Points E and F are moved in a similar manner along their respective triangle sides. Then we can observe how the triangle GHI is formed and changes shape depending upon how far Point D moves along Segment BC. (Click CLICK HERE for your own personal exploration with animation.)
If you took the time to explore with the above animation opportunity, you would get similar results as shown above and below. Notice in the above figure that when Point D is to the left of the midpoint of line BC, triangle GHI is formed with Point H on the right of the internal triangle.
If Point D is to the right of the midpoint, then the internal triangle flips over so that Point H is on the left side of the internal triangle. (Ignore the Animate block in the following figure.)
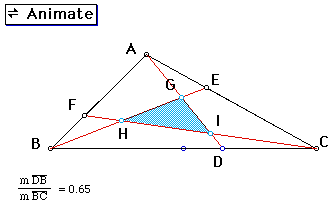
As a parenthetical remark, there will be a maximum, internal triangle when Point D is co-located either at Point B or Point C. This last remark should be intuitive. If it is not intuitive, then it is recommended to conduct the personal exploration as offered above. (CLICK HERE to go to the above place in this essay for the animation opportunity.)