A parametric curve in the plane is a pair of functions
where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t (work with parametric equations should pay close attention the range of t). In many applications, we think of x and y "varying with time t " or the angle of rotation that some line makes from an initial location.
Here is the graph of
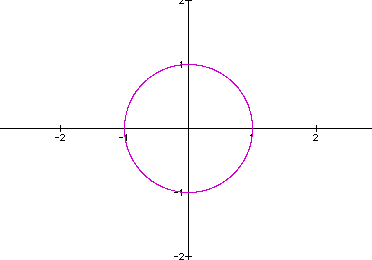
What if we change our parameter to ![]() ?
?
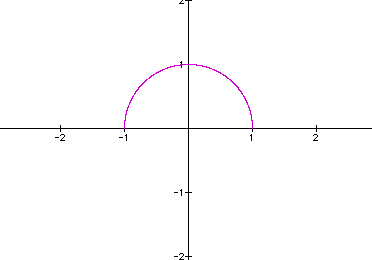
Let's examine why this happens. Consider a particular value
for t: zero. Then we have ![]() , or
, or ![]() ,
and thus the point (1, 0) is graphed. Now increase our particular
value of t to
,
and thus the point (1, 0) is graphed. Now increase our particular
value of t to ![]() . Then we have
. Then we have![]() ,
and thus the point (0, 1) is graphed. Use your calculator to find
some other points on this graph.
,
and thus the point (0, 1) is graphed. Use your calculator to find
some other points on this graph.
Get two points in each of the four quadrants and graph them on graph paper to turn in.
Email questions to me.
For various a and b, investigate
x = a cos (t)
y = b sin (t)
for ![]() .
Try a=1 and b=1, so we have the parametric equation
.
Try a=1 and b=1, so we have the parametric equation ![]() with a=1, b=1.
with a=1, b=1.
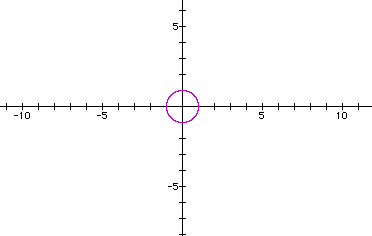
It's a circle, radius 1, center (0,0).
Now try a=2, b=2 in ![]() :
:
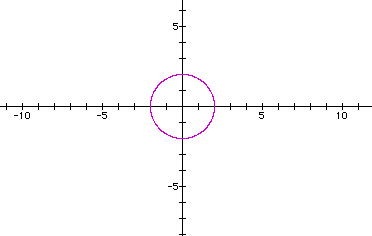
It's a circle, radius 2, center (0,0).
Now try a=1, b=2 in ![]() :
:
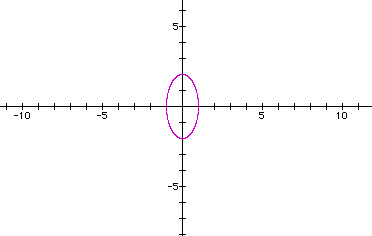
Now we have an ellipse, height 4, width 2, center (0,0).
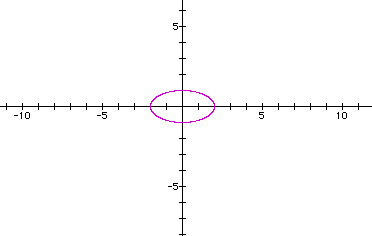
Now we have an ellipse, height 2, width 4, center (0,0).
Can you form a conjecture? What is your hypothesis? Use your
hypothesis to predict what the graph of ![]() will
look like with a=3, b=5. Email
your prediction.
will
look like with a=3, b=5. Email
your prediction.
What about noninteger values of t, say a=2.5, b=4.5? Will noninteger values fit your hypothesis? Here's the graph:
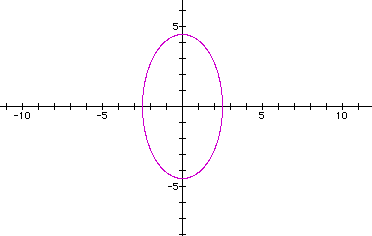
Does your hypothesis still hold?
What if one of the values is zero? Let a=0, b=4. What do you think the graph will look like? Use your hypothesis to predict.
Here's the graph:
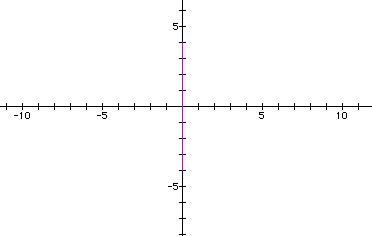
It's a line 0 wide and 4 tall. Does this fit your hypothesis? How about a=4, b=0?
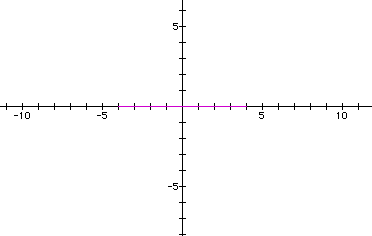
It's a line 4 wide and 0 tall.
Finally, what would the graph look like with a=0, b=0 and why? Email your answer.
RETURN TO HOME PAGE