USING SPREADSHEETS IN
MATHEMATICAL EXPLORATIONS
Spreadsheets can make the most of your time in an investigation. Imagine being able to do an experiment with any of several variables changing a the push of a button. You can evaluate your observations instantly, change a variable, and evaluate the new observations instantly!
Consider the Fibonnaci sequence. A spreadsheet makes the following investigations easily approachable.
Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence.
What happens as n increases?
What about the ratio of every second term?
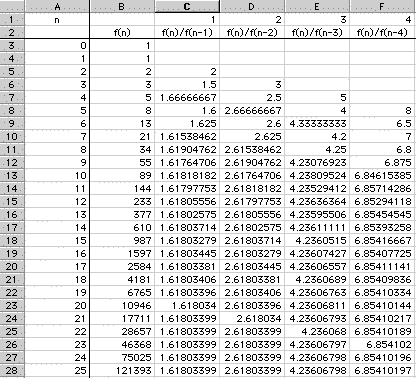
To begin, we construct the Fibonnaci sequence using Excel. Look here to examine the worksheet. Column B contains the Fibonnaci numbers f(n). Note that f(0)=1 and f(1)=1. The third Fibonacci number is calculated by adding the two previous Fibonacci numbers, 1 and 1. Look at cell B6 in the link to see a formula excel uses to accomplish this. This formula was then copied to the desired number of cells in column B.
Here is part of the spreadsheet:

Column C gives the ratio of any two adjacent Fibonacci numbers. As you can see, as n increases, this ratio approaches the golden ratio.
Column D gives the ratio of every 2nd Fibonacci number. That ratio approaches a number that is not recognizable at first. Interestingly, the ratio approaches the square of the golden ratio!
Column E gives the ratio of every third Fibonacci number. Can you guess what that ratio approaches? Answer: the cube of the golden ratio!
Column F gives the ratio of every fourth Fibonacci number. You already know what that ratio approaches; it approaches the golden ratio to the fourth power.
This pattern continues indefinitely (not proven here) and is shown on the spreadsheet all the way to identifying the ratio of every 11th Fibonacci number (and yes, the ratio approaches the golden ratio to the 11th power.)
Look around the spreadsheet and find formulas that were used to generate all of the numbers you see in the spreadsheet itself.
Try making your own spreadsheet that shows how much money you would have after 30 days if on day one you saved 1 cent, and each day after day one you saved twice as much as the day before. So day one you save 1 cent, day two you save 2 cents, day three you save 4 cents, etc. How much would you have after a week? two weeks? three weeks? a month? Are you suprised? (Look here if you just want to know!)
Now let's use spreadsheets to examine money! Savings and investment are easily investigated using spreadsheets. In the real world, spreadsheets help decision makers determine the best course of action to take given multiple variables and are probably the most used computer tool in business.
How much money would you have if you were given $5000 at age 21, then invested it in stocks (averaging 11%) until you retired? Look here under the tab labeled "one time invest". What do you think? Feel free to change the values in the grey.
| Amount of one time investment | Annual interest rate | Time invested in years | Your Nestegg |
| 5000 | 0.11 | 25 | 67927.3190145562 |
Not many of us are lucky enough to be given $5000, so let's look at a more likely scenario: Let's say you save$2000 per year from your job for 40 years. How much would you have then? (Assume an 11% return.) Look here under the tab labeled "save every year". Again, feel free to change the values in grey.
| Amount of periodic payment | Periodic interest rate | Periods invested | Your nest egg | Your investment | Interest Earned |
| -2000 | 0.11 | 40 | 1163652.13282911 | 80000 | 1083652.13282911 |
If you like, go to the tab labeled "various" and experiment with different amounts, periods, and interest rates. Determine what you must do to be a millionaire by retirement. How about a 2 millionaire?
Want to be a financial planner? Go here and change amount invested and interest rate for each year. Amaze your friends, astound your neighbors, just have fun predicting how your hard earned money will provide a comfortable retirement for you, if you save. Now you see why saving is so important!
Let's look at another way to use spreadsheets. This spreadsheet helps predict the amount of useable lumber (board feet) of any tree given its age.
The data available was put into a table and the spreadsheet created the chart. Next we had the spreadsheet create a function that closely imitates the data in the graph. Then we wrote a formula that included the function and a few adjustments. We can use this formula to enter the age of ANY tree and have board feet be estimated accurately. Try it yourself! Enter the age of a tree in cell A19 (grey) to see how many board feet that tree would yield.
What use can you think of that a spreadsheet could help you with?
RETURN TO HOME PAGE