,How can you predict the shape and placement of graphs of quadratic functions by inspecting their formulas? If you were asked to sketch the graph of
,what would you do?
This is a quadratic function in standard form
.
What shape is the graph? What are and where are any special points of the graph? What about intercepts, are they predictable? How does this graph change and move when you change the values of a, b, and c? Let's check it out.
We will graph several quadratic equations, systmatically changing the values of a,b, and c and observe changes in the graphs. We will hypothesize, test, and make conclusions based on these observations.
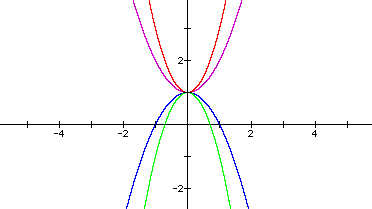
First we'll test different values of a=1,2,3, while b=0, c=0;
so we have 
(blue), 
(purple), 
(red)
on the same graph below.
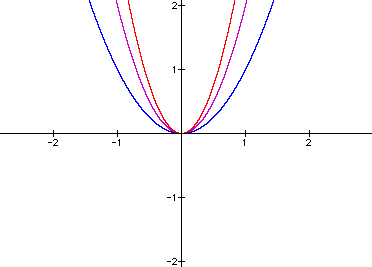
What can you conjecture about the value of a and the shape of the graph? What about the vertex? Test your hypothesis on a few examples with your grapher. Did you guess that the higher the number a, the skinnier the shape of he graph? That appears to be true from our observations.
Let's use our hypothesis to predict graphs with a = -1,-2,-3. According to our hypothesis, these graphs will be fatter than the graphs above (since -1, -2, and -3 are smaller than 1, 2, and 3).
(blue), 
(purple), 
(red)
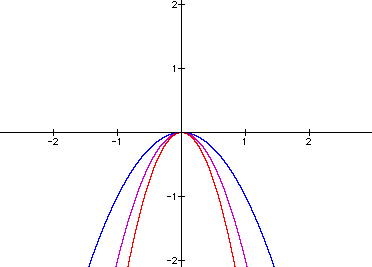
What happened? The vertices are still (0,0) but it seems we need to change our hypothesis in other respects. The smaller values did not create a fatter graph. In fact, it appears that when a = 1 and a = -1 the graphs have the same "fatness"; when a = 2 and a = -2 the graphs have the same "fatness"; and when a = 3 and a = -3 the graphs have the same "fatness".
What is different about the graphs when a changes sign? How can we adjust and/or expand our hypothesis to incorporate these new observations?
Well, what have we observed that is true
in all our observations in which our functions are in the form
? These will be our hypotheses.
1) when a is positive, the graph opens upward (smile)
2) when a is negative, the graph opens downward (frown)
3) "fatness" depends on the absolute value of a; the greater the absolute value, the skinnier the graph compared to a=1, and the lesser the absolute value of a, the fatter he graph compared to a=1.
4) the vertex is at (0,0) in equations of this form
Let's test our hypotheses by using them to predict what the graphs of a few quadratic functions look like Remember the value of a changes and the values of b and c are zero. Try a=-25 and a=.5. Using our hypotheses above, what will these graphs look like? (I've included the graph when a = 1 so that you may compare fatness.)
(blue),
(purple), 
(red)
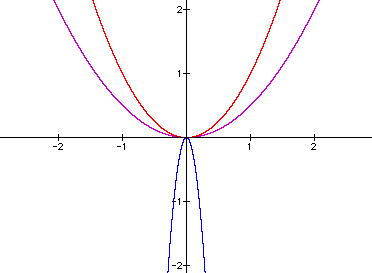
1) Determine whether our hypotheses hold.
2) Verify through algebra that the vertices are all (0,0).
3) What are the x and y intercepts (if any)of these two graphs.
Email your questions, answers AND reasons to me and be thorough!. Be sure to indicate that you're working on PART 1 of lesson 2.
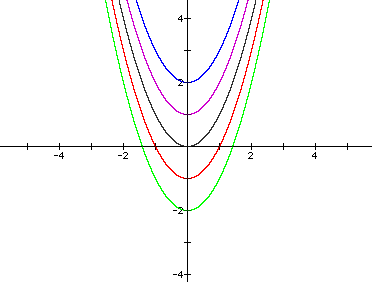
Now let's look at how the graph of 
moves and changes with a=1 and c varying while b stays at 0. This
way we should see what effect c has on the graph. Some equations
in that form are:
(blue),
(purple),
(black),
(red),
(green)
Now let's see what happens when we vary a: Some equations are:
(purple),
(red),
(blue),
(green)
By sketching, predict the shape and vertex
of:
and 
. You
should be able to sketch these graphs quickly. Here is a check
for you
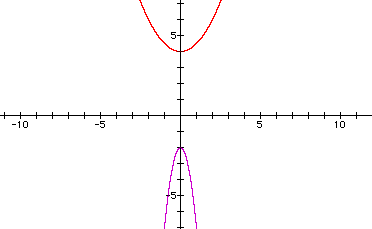
What happened to our graph as we varied c?
What happened when we varied a and c ? What is the vertex
of each graph? How is the vertex related to the value of c when
equations are in this form? What hypotheses can you make about
graphs of the form 
?
Write and test your hypotheses with 5 equations
that are in the form above. Be sure to include a few non-integer
values for a and/or c. You should sketch the graphs as part of
your investigation. After testing your hypotheses, write some
conclusions about equations in the form of 
and
their shapes and vertices.
Email your questions and conclusions to me.
Finally, what do you think will happen to our
graph of 
as we begin varying b? Let's keep
a and c constant to begin with - that way we can see what effect
b has on the graph. A few equations of that form are:
(red),
(purple),
(blue),
(green)
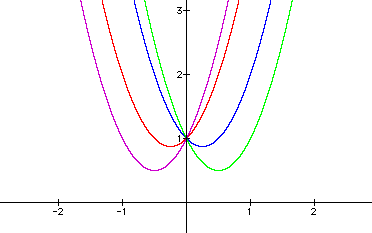
You can see from these graphs that a change
in b does have a particular effect on the placement of the vertex
of the graph. (Use the animate function in your grapher
with 
and 
to see
this effect.) However, it may not be clear yet how to use this
information to predict the coordinates of the vertex. Let's look
at a few more graphs before we try a conjecture about values of
b and vertex coordinates.
(green), 
(purple)
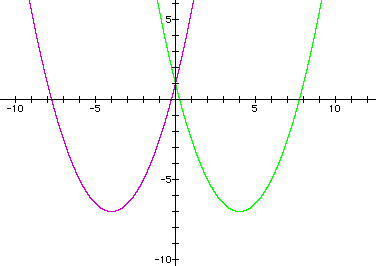
The vertex of the purple graph is (-4,-7).
The vertex of the green graph is (4,-7).
Now try 
(red) and 
(blue).
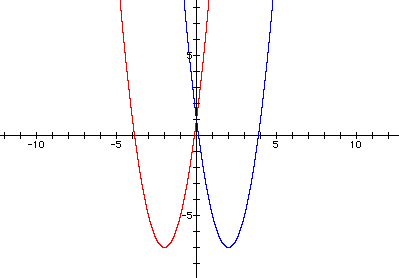
The vertex of the red graph is (-2,-7).
The vertex of the blue graph is (2,-7).
Finally try 
(red), 
(purple).
The vertex of the red graph is (1,-11).
The vertex of the purple graph is (-1,11).
Some of you may have come up with a way to predict the coordinates of the vertex of a quadratic in this form and may email your idea to me (include an example or two), but it is still not very clear how to do this.
Let's summarize what we know:
when a is positive, the graph opens upward (smile)
when a is negative, the graph opens downward (frown)
fatness depends on the absolute value of a; the greater the absolute value, the skinnier the graph compared to a=1, and the lesser the absolute value of a, the fatter he graph compared to a=1.
But we still need a way to get the vertex of quadratic graphs. Let's summarize what we know about vertices of quadratic equations.
If the quadratic is in the form 
,
we know the vertex is at (0,0). You
should verify this using a few examples on your grapher.
If the quadratic is in the form 
,
we know the vertex is at (0,c). You
should also verify this using a few examples on your grapher.
If the quadratic is in the form 
,
it is not yet clear where the vertex is. Some of you may have
seen that the x coordinate of the vertex may be calculated by
. Go back to our earlier examples
to see if this formula for the x coordinate of the vertex works
for all forms of quadratic equations. Check each type of equation.How
would you then get the y coordinate of the vertex?
Email your ideas and questions to me along with the question to which you are resonding.
Now let's list the four ideas you have investigated and verified:
- when a is positive, the graph opens upward (smile)
- when a is negative, the graph opens downward (frown)
- fatness depends on the absolute value of a; the greater the absolute value, the skinnier the graph compared to a=1, and the lesser the absolute value of a, the fatter he graph compared to a=1
- the coordinates of the vertex are (
, f(
)) where f is your
quadratic function.
Assignment:
1) List the four or five things we know about graphs of quadratic functions by looking at their formulas.
2) Besides observation, how could you have come up with this formula for the vertex by using the quadratic formula? Hint: how many solutions does a quadratic equation have when the discrimant is negative, positive, zero? Email your assignment to me. Label it "vertices of quadratic functions".
3)Go back through our examples and put EACH
quadratic into standard form 
. Is
it easier to use standard form to determine the vertex? Why?
RETURN TO HOME PAGE