We have seen the relationship between the vertex
of a quadratic function and the quadratic formula; specifically,
when the discriminant is zero, there is exactly one solution (root)
to the quadratic function which must be the vertex of the graph
of the function. We saw that the vertex of a quadratic function
may be found by using this fact and solving ![]() .This
is true by algebra; the quadratic formula yields only one root
when the discriminant is zero. Try it! Write the quadratic formula
and make the discriminant zero. What do you end up with?
.This
is true by algebra; the quadratic formula yields only one root
when the discriminant is zero. Try it! Write the quadratic formula
and make the discriminant zero. What do you end up with?
But what about other aspects of the quadratic
formula? How can we see those by using graphs? Let's look at the
graph in the xb plane of ![]() .
.
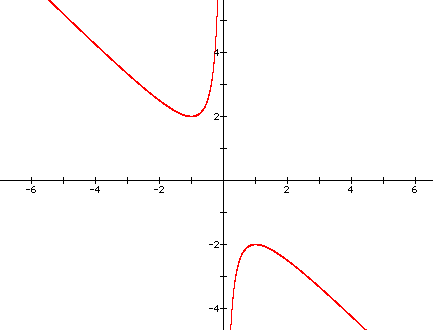
Now we draw a line straight through the vertices
of both legs of the hyperbola. The equation of that line is ![]() . (You will learn in calculus how to find
the equation of this line.) Now we add the line to our graph.
. (You will learn in calculus how to find
the equation of this line.) Now we add the line to our graph.
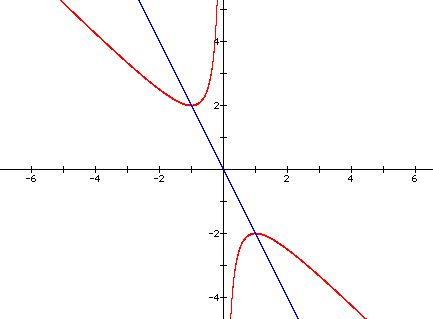
To inspect the quadratic formula, let's look at the roots at y=5. We now add the line y=5 to our graph and examine just the upper leg of the hyperbola where our roots are.
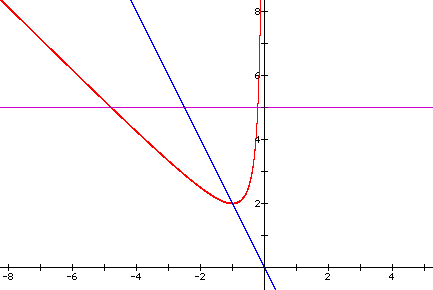
From the graph we can see that there are two roots at y=5, but it is not clear from the graph exactly what the roots are. It also appears that the blue line is equidistant from either side of the hyperbola at any particular y>=2. We will prove that this is true and we will show how this distance is is related to the quadratic formula.
What are the coordinates of the vertex of the upper leg of this hyperbola? Well, this is a quadratic function, so the vertex may be found using the same method as with a parabola. (You will get two values when you do this. We will only use the value that corresponds to the upper leg of our hyperbola; discard the other answer.)
1) What is the x coordinate of the vertex of the upper leg of the hyperbola?
2) What is the y coordinate of the vertex of the upper leg?
3) Is the blue line that goes through the vertex equidistant from both sides of the upper leg of the hyperbola at the vertex?
4) What is the distance from the blue line to the hyperbola at the vertex?
5) Is this the outcome you expected? Why?
Email your questions and answers.
Recall our graph:

Look at the point of intersection of the blue and purple lines. Is this point equidistant from the sides of the hyperbola? How can we find out?
Find the coordinates of this point of intersection by equating the equations for these lines. First get both equations equal to zero. (What property allows us to do this?)
Solve for x, then use the x value to solve for y. You should get that the lines intersect at the point (-2.5, 5).
Later we will solve
a general case, but
for now solve for the points of intersection of the line y=5 and the
hyperbola.
(Substitute y=5 into the equation for the hyperbola, then use
the quadratic formula.) You should get the points (![]() ,5)
and (
,5)
and (![]() ,5). If you are using a calculator,
you may keep using these exact values. If you are working by hand,
change these to decimal approximations. Then you have the points
(-4.79129, 5) and (-.208712, 5).
,5). If you are using a calculator,
you may keep using these exact values. If you are working by hand,
change these to decimal approximations. Then you have the points
(-4.79129, 5) and (-.208712, 5).
Let's look at our graph again, with the coordinates of interest labeled.
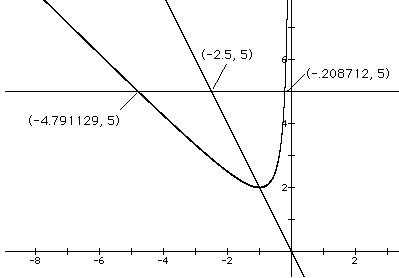
Now we must see if the point (-2.5, 5) is equidistant from the other two labeled points. Use the distance formula to make this determination.
![]() = 2.29129.
= 2.29129.
![]() = 2.29129.
= 2.29129.
So the distances ARE the same. The line 2x+y=0 is equidistant from both sides of the hyperbola at y=5.
Using algebra, find the coordinates of the point of intersection of 2x+y=0 and y=5 to be (-2.5,5).
Now consider the line y=0. The points at which the hyperbola or parabola intersect the line y=0 are the roots of the quadratic.
For example, take the quadratic
![]() .The equation of the line equidistant from
the sides of the graph is 6x+4=0:
.The equation of the line equidistant from
the sides of the graph is 6x+4=0:
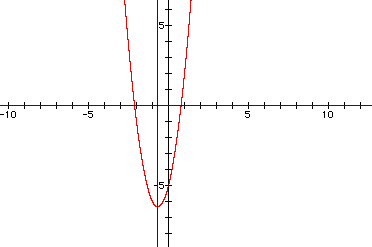
What are the roots of this equation?
Where are the roots in relation to the intersection
point of 6x+4=0 and y=0 (the x axis)?
Now move to a general case. Take ![]() as our quadratic. The line equidistant from each side of the hyperbola
or parabola is 2ax+b=0. What are the roots of this quadratic?
That is, where does
as our quadratic. The line equidistant from each side of the hyperbola
or parabola is 2ax+b=0. What are the roots of this quadratic?
That is, where does ![]() intersect the line
y=0 (the x axis)?
intersect the line
y=0 (the x axis)?
We hypothesize that the roots we're looking for will be equidistant from the point where the line 2ax+b=0 intersects the line y=0 (the x axis), so we first find this point.
We solve the equation 2ax+b=y with y=0 since
we are on the x axis. Then we have 2ax+b=0 and finally, x= ![]() . So the coordinates of the point equidistant
from the roots on the line y=0 are (
. So the coordinates of the point equidistant
from the roots on the line y=0 are (![]() , 0).
, 0).
Now we solve for the points of intersection
of the graph and the line y=0. We do this as before, by setting
y=0 (instead of y=5 as above) and solving for x. Then we have ![]() .
.
We will not use the quadratic formula to solve this equation. Instead, we will complete the square to solve for x. Try this on your own if you like.
So we find that the x coordinates of the points of intersection come from the quadratic equation!
For kicks, use the distance formula to verify
that the distance from x = ![]() to either of the
x coordinates we just found is the same. Email
your findings to me.
to either of the
x coordinates we just found is the same. Email
your findings to me.
RETURN TO HOME PAGE