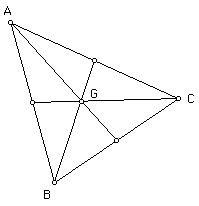
1) The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. Here's an example.

The centroid G is the point of intersection of segments joining the vertices and opposite midpoints.
2) The ORTHOCENTER (H) of a triangle is the common intersection
of the three lines containing the altitudes. An altitude is a
perpendicular segment from a vertex to the line of
the opposite side. Here is an example of a constructed orthocenter:
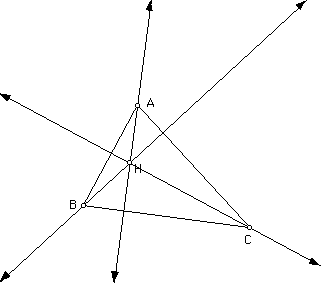
H is the orthocenter of triangle ABC.
3) The CIRCUMCENTER (C) of a triangle is the point in the plane
equidistant from the three vertices of the triangle. Since a point
equidistant from two points lies on the perpendicular bisector
of the segment determined by the two points, C is on
the perpendicular bisector of each side of the triangle. Note:
C may be outside of the triangle. Here is a constructed circumcenter.
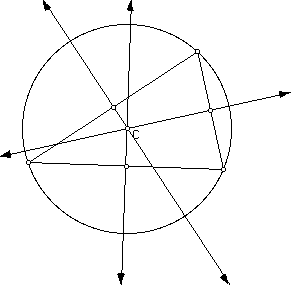
C is the circumcenter of this triangle.
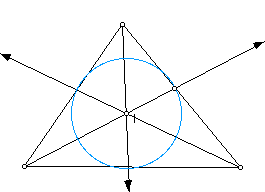
4) The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle. Below, the incenter is labeled as the center of the lue circle.
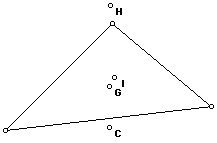
Many peculiarities emerge while experimenting with this in GSP:
I and G are always inside the triangle or on a side, while C and H can be inside, outside, or on a side.
H always passes through a vertex when going from inside to outside or visa versa, but C always passes through a midpoint of a side when going inside to outside or visa versa.
C, H, and G are always collinear.
It seems that H, I, G, and C are collinear when the triangle is isosceles.
6) Construct a triangle connecting the three midpoints of the sides. This is called the MEDIAL triangle. It is similar to the original triangle and one-fourth of its area. Construct G, H, C, and I for this new triangle. Compare to G, H, C, and I in the original triangle.
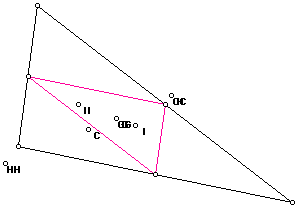
In this sketch, the larger triangle has centers labeled with double letters, while the smaller triangle has single letter labels.
7) Take any acute triangle. Construct a triangle connecting
the feet of the altitudes. This is called the ORTHIC triangle.
Construct G, H, C, and I for the orthic triangle. Compare to
G, H, C, and I in the original triangle. Can you extend this to
right triangles or obtuse triangles?
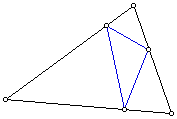
The orthic triangle does not extend to right triangles since the feet of two of the altutudes make only one point, leaving a degenerate orthic triangle.
The orthic triangle does not extend to obtuse triangles since obtuse triangles have altitudes that meet outside of the parent triangle.
8) Take an acute triangle ABC. Construct H and the segments HA, HB, and HC. Construct the midpoints of HA, HB, and HC. Connect the midpoints to form a triangle. Prove that this triangle is similar to triangle ABC and congruent to the medial triangle. Construct G, H, C, and I for this triangle. Compare.
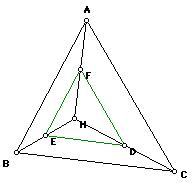
AB is parallel to FE since F and E are midpoints of sides of triangle AHB. Hence, angle HFE and angle HAB are congruent (parallel lines cut by a transversal have congruent corresponding angles). Similarly, angle HEF and angle HBA are congruent. Thus triangle HEF and triangle HBA are similar by angle-angle.
This green triangle appears to be congruent to the medial triangle (red).
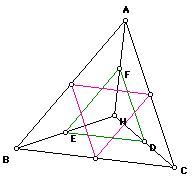
9) In the same original triangle, construct the three secondary
triangles of Exercises 6, 7, and 8. Construct the circumcircle
for each of the secondary triangles. What do you observe?
Can you prove your conjecture?
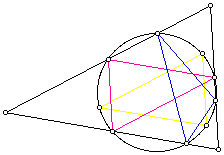
All three secondary triangles have the same circumcircle, so they all have the same circumcenter. All nine vertices of the three triangles lie on their circumcircle.
10) The Nine-Point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to orthocenter. Construct the nine points, locate the center (N) and construct the nine point circle.
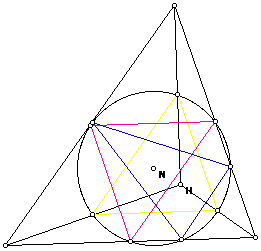
The center of the nine point circle is the center of the circumcircle of any of the secondary triangles. Alternatively, the nine point circle can be constructed by finding the midpoint N of the segment joining orthocenter H and circumcenter C, then constructing a circle from that point N to any point on the nine point circle:
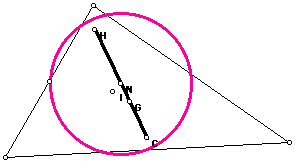
11) How is N related to G, H, C, or I for different shaped triangles?
N is collinear with G, H, and C at all times, as N is by definition the midpoint of the segment containing H and C, and G also lies on this line. It appears that N is collinear with these other points only when the triangle is isosceles.
12) Prove that the three perpendicular bisectors of the sides
of a triangle
are concurrent.
Consider triangle ABC with side midpoints D,E,F as below.
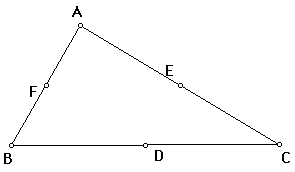
Now the perpendicular bisector of side AB is the set of all points equidistant from points A and B.
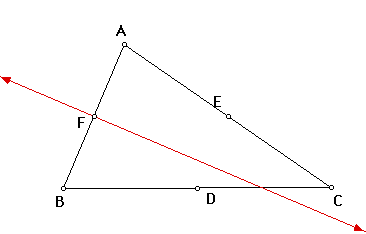
And the perpendicular bisector of side AC is the set of all points equidistant from points A and C.
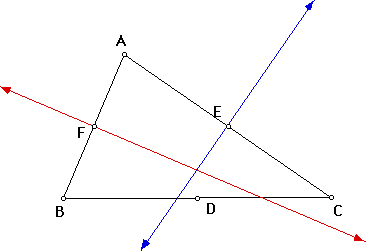
Clearly these lines will intersect, as they cannot be parallel. Their point of intersection is a point that is equidistant from B, A, and C. (Interestingly, this must also then be the circumcenter.) Now the perpendicular bisector of side BC is the set of all points equidistant from points B and C.
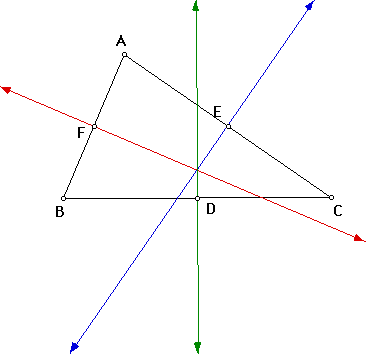
But we already know that the point of intersection of the first two perpendicular bisectors constructed (red and blue lines) contains a point that is equidistant from B and C (and A).
So the line that contains the set of ALL points equidistant from B and C (i.e. the perpendicular bisector of side BC) must contain the point of intersection of the red and blue lines, and thus the perpendicular bisectors are proven concurrent.
RETURN TO HOME PAGE