1. Make a script for construction of the tangent circles.
To run the script, you must select, in the following order, only four points:
1) point on 1st circle
2) center of 1st circle
3) point on second circle
4) center of 2nd circle
All four points must be selected and they must be selected in the order above! The tangent circle appears in red, tangent to the point selected on the first circle and tangent to the second circle wherever.
Click here to experience the script yourself.
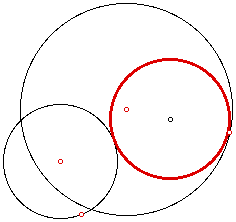
Here's an example:

This script seems to work regardless of the placement of the two circles. That's the way it should be.
2. Construct the tangent circle to two given circles if the
given point
is on the smaller of the two circles
a. so that the smaller circle is external to the tangent circle.
b. so that the smaller circle is internal to the tangent circle.
This should be cake if my script works.....
a.
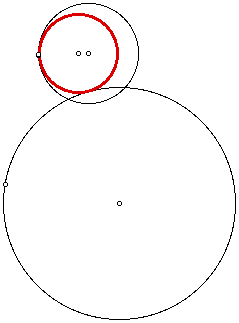
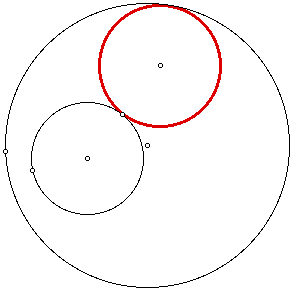
In both cases above, the smaller circle is external to the tangent circle.
b.
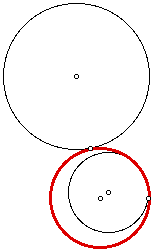
And above, the smaller circle is internal to the tangent circle. This took some experimentation. I found it interesting that both situations can easily be found using a single sketch by moving the point on the first circle (the first point selected) around the circumference. It may be hard to visualize, so try this yourself by clicking here.
After creating your red tangent circle, move the point of tangency of the first circle around it's curcumference. Go slowly, and watch what happens.
4. Discuss the loci of the centers of the tangent circles for both 2a and 2b.
In 2a, the smaller circle is outside of the tangent circle. The locus of the tangent circle is an ellipse. Go here to check it out. Pull point E around circle c1. Point X will be traced. It trace is in the shape of an ellipse.
Next, try moving point Z around until the smaller circle is inside the red tangent circle.
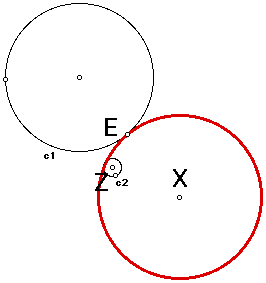
Now pull point E around circle c1. Now the locus is a hyperbola! Play until you're satisfied that each time the small circle is outside the red tangent circle, the locus of the center of the red tangent circle is an ellipse AND each time the small circle is outside the red tangent circle, the locus of the center of the red tangent cirle is a hyperbola.
When the circles intersect, the tanget circle is always inside one of the circles.
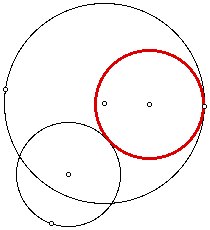
The tangent circle may also be inside of one of the circles if one circle contains another.
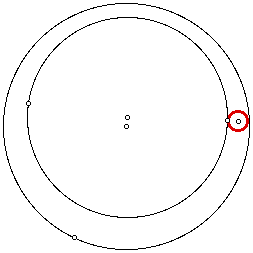
If the two circles do not intersect, then the red tangent circle contains one of the circles (except at one instant when only a line is tangent to both circles).
If the two circles do intersect, the red tangent circle is contained by one of the circles.
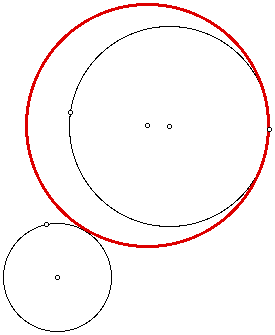
6. Discuss the locus of the centers of the constructed tangent circles when the two given circles intersect.
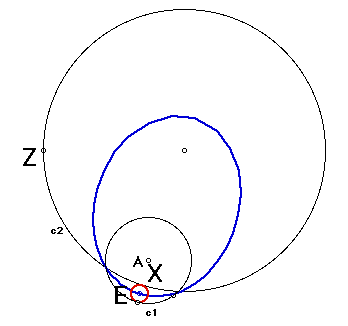
It seems that the locus of the center of the tangent circle is an ellipse when the circles intersect. Here's how to look at it yourself:
Click here.
Select point X, point E, and circle c1, in that order.
Go to construct menu and choose locus.
Select point X and go to display menu and turn off trace point.
Select point E and point A, then use point A to pull circle c1 around to different places that have circle c1 intersecting circle c2.
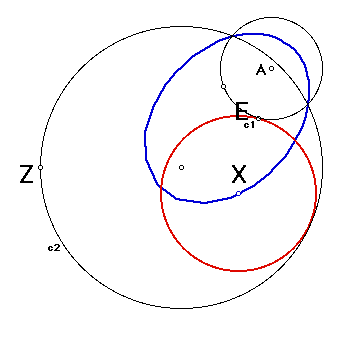
Or,
7) Discuss the construction of the circles tangent to two given circles when two circular regions are disjoint. Look for all cases.
Since the circles are disjoint, must the red tangent circle must be larger than either of the two circles? No. But that's the way my script seems to work.
Exactly when does the tangent circle not exist? Only when the line tangent to both circles is a straight line. This happens when? This happens only when both points of tangency lie on a line normal to the line containing the diameters of the respective circles which contain the points of tangency AND the two circles lie in separate half- planes defined by that line. The criteria is not met in the examle below, as both points of tangency do not lie on the line described above.
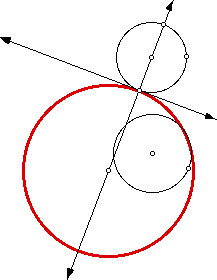
In the following example, the criteria is not met, as both circles do not lie in separate half- planes defined by the normal line.
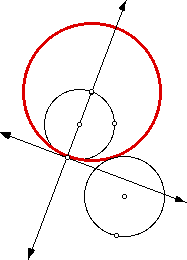
But in the next example, the criteria IS met, as both points of tangency lie on the line perpendicular to the line the center of the circle to the point of tangency for each respective circle.
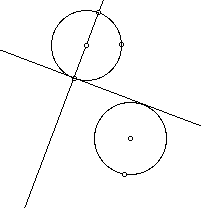
The red tangent circle does not appear here, as it does not exist at this instant. Check this out yourself here. Grab the radius of circle c1 to experiment.
Another note, this is an if and only if relation. The tangent circle to two disjoint circles becomes a line if and only if both points of tangency lie on the line normal to the points of tangency. That is, if the circle tangent to two disjoint circles becomes a line, then the points of tangency lie on a line normal to the points of tangency AND if the points of tangency lie on a line normal to the points of tangency, then the circle tangent to the disjoint circles becomes a line.
RETURN TO HOME PAGE