Euclid's work will live long after all the text books of the present day are superseded and forgotten. It is one of the noblest monuments of antiquity.

Sir Thomas L. Heath (1861-1940)

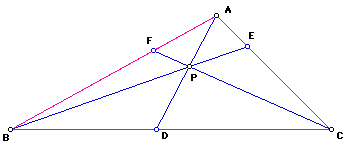
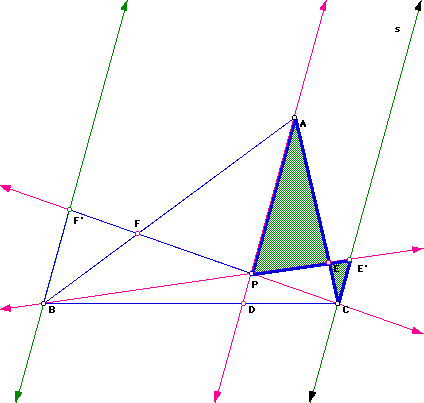
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

Explore (FA)(BD)(EC) and (FB)(DC)(AE) for various triangles and various locations of P.

Using GSP, we can easily calculate these products.

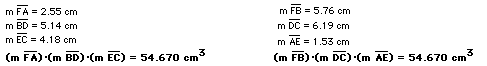
What do you notice?

We want to see if these products will be equal for various triangles and various locations of P.

Click here for a GSP demonstration for various locations of P.

Click here for a GSP demonstration for various sizes of triangle ABC.

Based on the GSP animations, what is the relationship between (FA)(BD)(EC) and (FB)(DC)(AE)?

We claim the following conjecture:

Proof:

The proof considers constructing parallel lines to produce similar triangles.

Construct line r parallel to line AP going through point B and line s parallel to line AP passing through point C. Label the point of intersection of lines r and CP as F ' and the point of intersection of lines s and BP as E '.

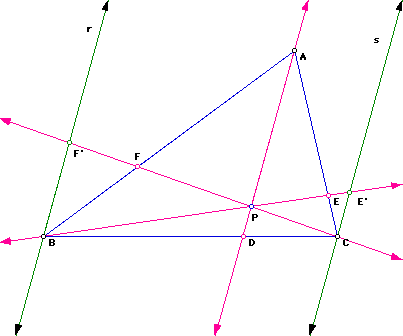
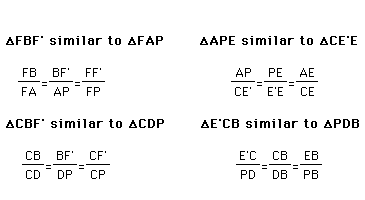
Next, we need to identify the similar triangles. The following pictures illustrate the four sets of similar triangles needed in this proof:

Triangle FBF ' is similar to Triangle FAP

Triangle APE is similar to Triangle CE'E

Triangle CBF ' is similar to Triangle CDP

Triangle E'CB is similar to Triangle PDB

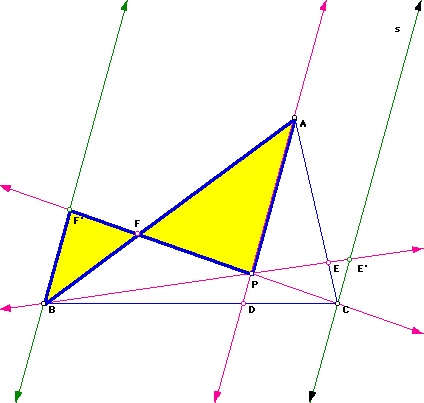
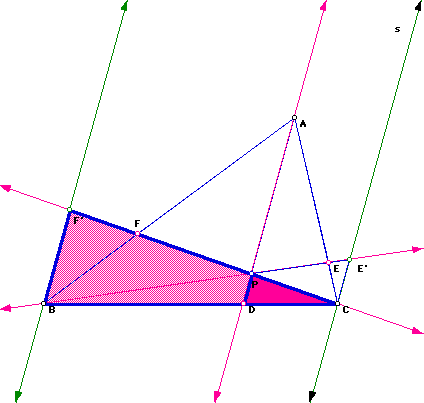
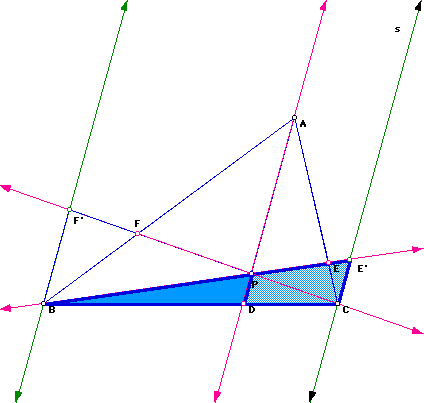
We know two triangles are similar if corresponding angles are congruent and the corresponding sides are proportional segments. Using this definition of similar triangles we can set up the following proportions for each set of similar triangles.

Consider the ratio

.

If we can show

then it follows that

Begin by making substitutions for each part in the ratio

.

Using the corresponding sides from the first set of similar triangles, we get

.

From the second set of similar triangles, the corresponding sides needed are

.

So making the appropriate substitutions we get the following new ratio

.

We still need to make substitutions for BD and DC. It is important to make the appropriate substitutions for BD and DC so that when replaced the ratio will simplify algebraically to 1.

Using the corresponding sides from the third and fourth last set of similar triangles, pick proportions that involve BD and DC and other common sides such as PD. The most beneficial proportions to pick are

.

Next, solve for CD and DB algebraically.

Now substitute what we have found for DC and BD into the ratio

and we get the following

.

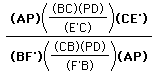Lo and behold, after simplifying this ratio algebraically,

.

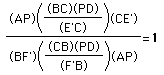Therefore, it follows that

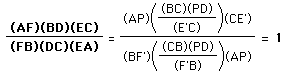
and