Many of the proofs in mathematics are very long and intricate. Others,
though not long, are very ingeniously constructed.
E. C. Titchmarsh (1899-1963)
We want to show that the three perpendicular biectors of the sides of
a triangle are concurrent.
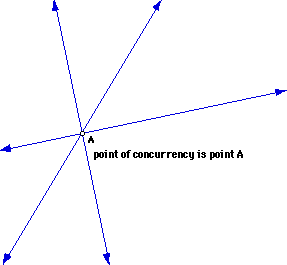
First it is important to understand the concept of concurrency.
Concurrent lines (segments or rays) are lines which lie in the same
plane and intersect in a single point. The point of intersection is the
point of concurrency. For example, point A is the point of concurrency.
The following is an interactive proof using GSP.
To proceed, click on each Step of the proof. If you want to retrace
your steps you may undo your previous step by clicking on the Undo Step.
Claim:
The three perpendicular bisectors of the sides of a triangle are concurrent.
Proof:
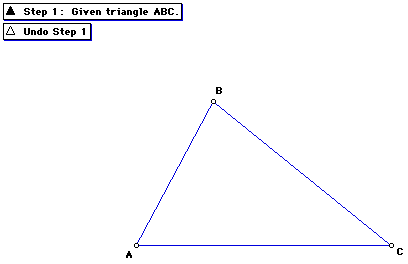
Step 1:
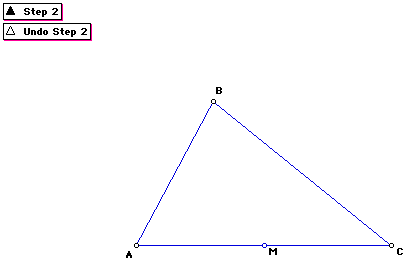
Step 2
Construct the midpoint of segment AC. Label the midpoint of AC as M.
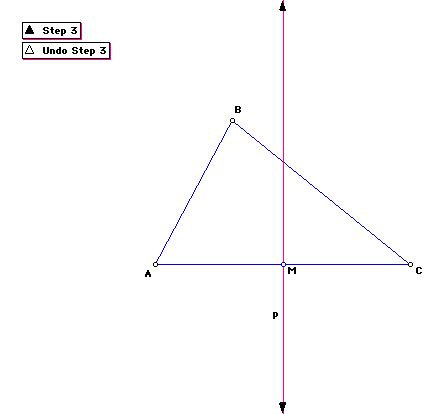
Step 3
Construct the perpendicular bisector of segment AC. Call the perpendicular
bisector p.
Step 4
Construct any point K on the perpendicular bisector p.
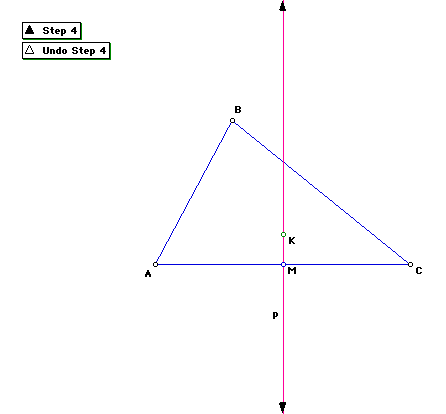
Step 5
Construct segment AK and segment KC.
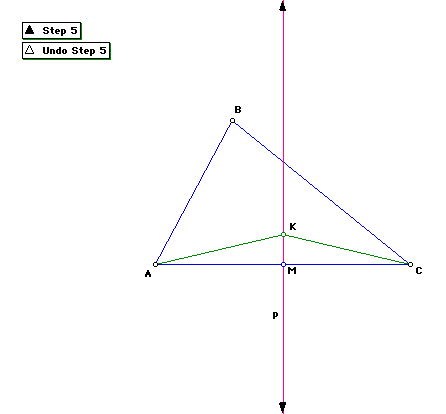
AM=MC by definition of midpoint.
KM=KM by the reflexive property.
Angle AMK and angle CMK are cut by a perpendicular line, p. Hence, the angles
are right angles and are both equal to 90 degrees. So, m<AMK = m<CMK
and angle AMK is congruent to angle CMK.
Now, triangle AMK is congruent to triangle CMK by SAS.
By CPCTC, AK=KC.
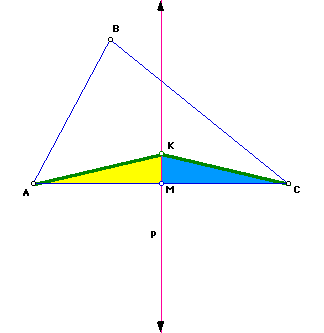
Step 6
Construct the midpoint of segment AC. Call it M'.
Construct the perpendicular bisector of AC. Label as q.
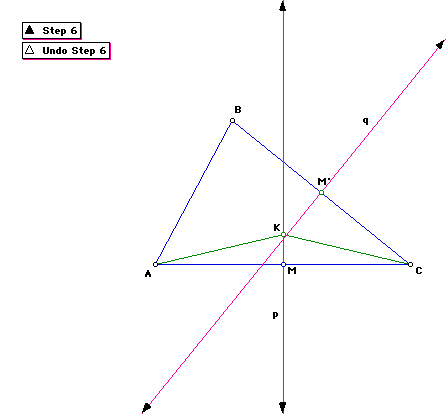
Since AC and BC are not parallel, the perpendicular bisectors, p
and q, must also intersect.
Let point K be the point of intersection.
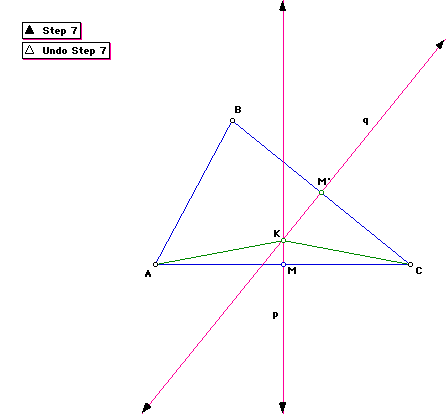
Step 7
Constuct point K as the point of intersection of p and q.
Step 8
Construct segment BK.
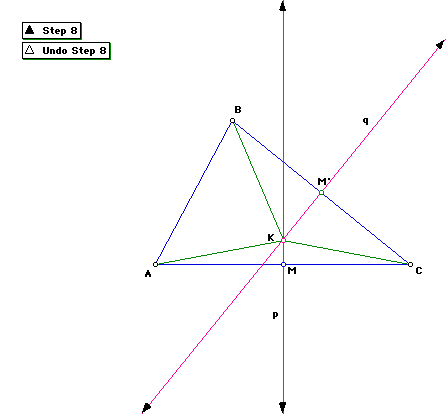
KC=BK using similar reasoning in Step 5. We know AK=KC. So by substitution
AK=KC=BK.
Furthermore, K is taken to be the intersection of the perpendicular bisectors
p and q.
Since K is on the perpendicular bisectors p and q, it must
also lie on the perpendicular bisector of AB.
Therefore, K is on the perpendicular bisector of AB.
Since K lies on the perpendicular bisectors of AC, BC, and AB, K is the
point of concurrency.
Hence, we have proved that the three perpendicular bisectors of the sides
of a triangle are concurrent.
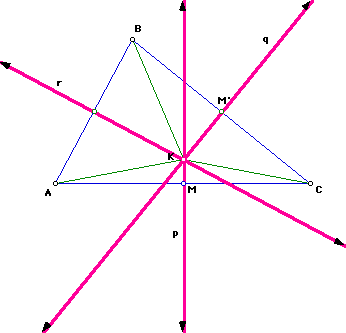
The following shows the construction of the perpendicular bisector of AB,
labeled as r.
The picture shows K to be the point of concurrency.
Extension
This proof can extend to other concepts such as the circumcenter
and circumcircle.
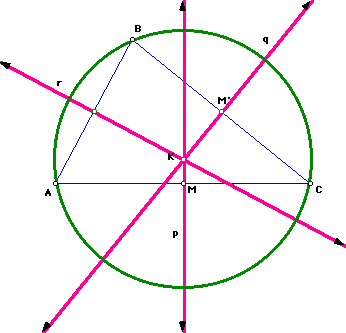
K, the point of concurrency, is also the circumcenter. The circumcenter
is the center of the circumcircle. The circumcircle is the circumscribed
circle of the triangle.
The following shows the cirumcircle of triangle ABC with circumcenter as
point K.
Return to Final Project Page












