Christopher Morley (1890-1957)
To construct the nine point circle of a triangle, follow these steps.
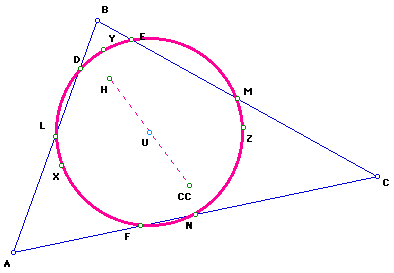
1. Draw a triangle ABC.

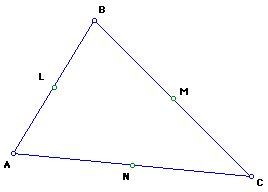
2. Construct the midpoints of the three sides. Label them as L, M, N.
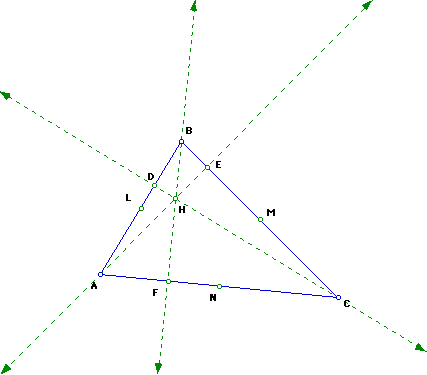
3. Construct the feet of the altitudes of the triangle ABC. Label them as
D, E, F. Label the point of intersection of the three altitudes as H. This
is also called the orthocenter.
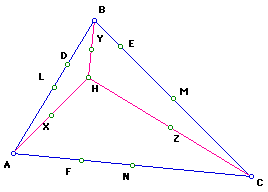
4. Construct the midpoints of the segments AH, BH, CH. Label them as X,
Y, Z.
First, notice the nine points, L,M,N,D,E,F,X,Y, Z, lie in a circle.
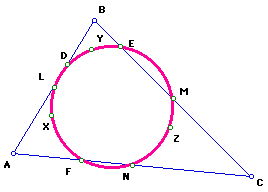
This circle is called the Nine-Point Circle.
To find the center of the Nine-Point Circle, construct the circumscribed
circle for triangle LMN. Label the center as U.
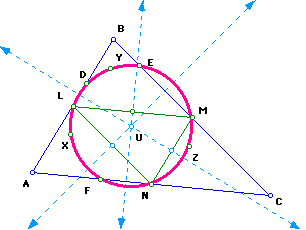
The center of the circumscribed circle for triangle LMN will also be the center of the Nine-Point Circle labeled as U.
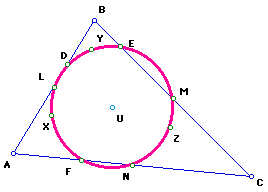
A second way to find the Nine-Point Center is to begin by constructing the circumcircle for triangle ABC. Label the circumcenter as CC.
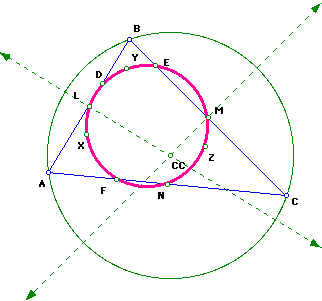
The center of the Nine-Point Circle, U, is the midpoint from the orthocenter, H, and the circumcenter, CC, of triangle ABC.
No matter what type of triangle we have, other than a degenerate triangle,
those nine points will always lie in a circle, the nine point circle,
with center at U.
For a complete demonstration, click the animate
button. Enjoy.
For a GSP Script that makes the Nine-Point Circle, click here.