The Eight-Point Circle and the Nine-Point
Circle:
Mathematical History Overlooked
William Shakespeare (1564-1616)
(The Tempest, Act I, Scene 2)
In February 1944, Louis Brand, a mathematician from the University of Cincinnati, duly noted in The American Mathematical Monthly, that the famous theorem on the Nine-Point Circle is actually a special case of a simple theorem on the Eight-Point Circle.
The theorem on the Eight-Point Circle states
When the diagonals of a plane quadrilateral are perpendicular, the mid-points of its sides, and the feet of the perpendiculars dropped from the mid-points on the opposite sides, all lie on a circle described about the mean center of the vertices.
The following is a prof the Eight-Point Circle Theorem taken directly from the article in The American Mathematical Monthly .
Proof.
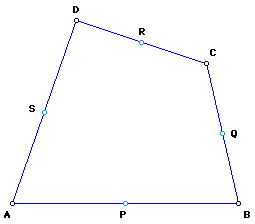
In the quadrilateral ABCD, let P, Q, R, and S denote the mid-points of the sides AB, BC, CD and DA.

It follows that PQRS is a parallelogram whose sides are parallel to the diagonals AC and BD of the quadrilateral ABCD. (Click here for a proof of this theorem).
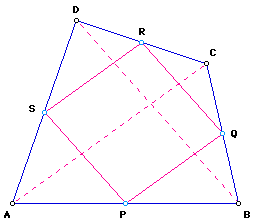
Now let the diagonals of the quadrilateral be perpendicular. Hence, when AC and BD are perpendicular, PQRS is a rectangle, its diagonals bisect each other at M, called the mean-center of the points A, B, C, and D (their centroid when each point has the weight 1).
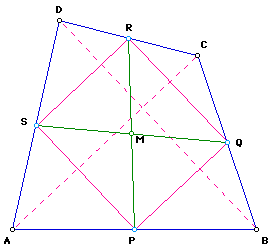
Therefore, P, Q, R, and S lie on a circle centered at M. If perpendiculars from P, Q, R, and S are dropped to the opposite sides (called altitudes), then the feet of the altitudes P', Q', R', and S' will also lie on this circle. Thus, the eight points, P, Q, R, S, P', Q', R', S' lie on a circle, called the Eight-Point Circle. Therefore, we have proven the theorem of the Eight-Point Circle.
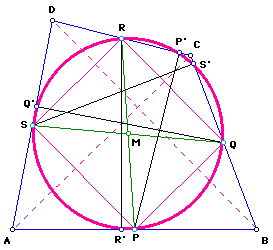
Now it becomes necessary to make the connection between the Eight-Point Circle and the Nine-Point Circle. Their geometric relationship is quite interesting, amazing and beautiful.
Suppose we focus our attention on triangle ABC. Construct the orthocenter of triangle ABC. Label as H.
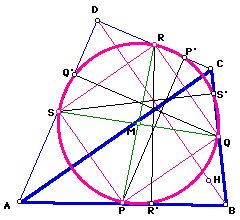
It may be helpful here to clean up the figure and hide unnecessary segments. The following figure is clearer to understand.
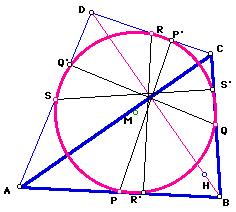
Now, suppose we take the vertices D of the quadrilateral ABCD and translate (map) point D onto point H. What happens?
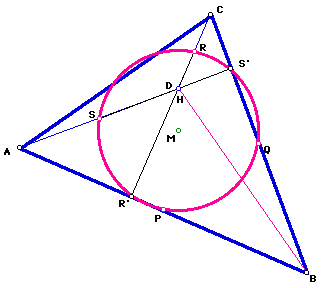
Notice from the figures above, P' becomes R' and Q' becomes S'. So each point is interchangeable.
Why does this happen? Look at quadrilateral ABCHA (see figure below). P, Q, R, and S are the midpoints of the sides of ABCHA. When you drop the altitudes from the midpoints, P, Q, R, and S to the opposite sides, it is clear that P' becomes R' and Q' becomes S'. Since those two points are one in the same, the eight points reduces to six points. But you still have the Eight-Point Circle.
To summarize, the Eight-Point Circle for quadrilateral ABCHA has reduced to a six-point circle. The six points are P, Q, R, S, P'=R', Q'=S'
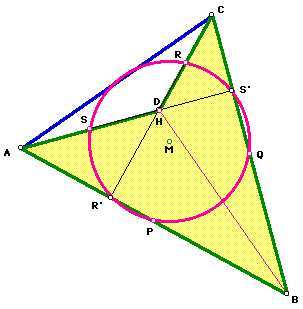
In a similar manner, suppose we look at quadrilateral BCAHB. S, T, Q, U are the midpoints of the sides of BCAHB. When you drop the altitudes from the midpoints, S, T, Q, U to the opposite sides, labeled as S', T', Q', U' respectively, it is clear that Q'=S' and U'=T'. Since those two points are one in the same, the eight points reduces to six points. But you still have the Eight-Point Circle.
To summarize, the Eight-Point Circle for quadrilateral BCAHB has reduced to a six-point circle. Those six points are S, T, Q, U, Q'=S', T'=U'.
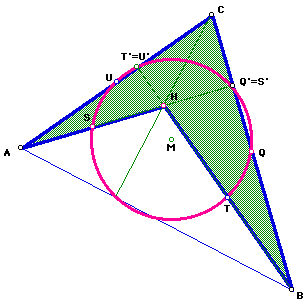
If you compare the last two figures (look closely), we have picked up three more points on the circle that were not on the original one (from quadrilateral ABCHA). Those three points being T, U, T'=U'.
Similarly, suppose we look at quadrilateral CABHC. P, T, R, U are the midpoints of the sides of CABHC. When you drop the altitudes from the midpoints, P, T, R, U to the opposite sides, labeled as P', T', R', U' respectively, it is clear that P'=R' and U'=T'. Since those two points are one in the same, the eight points reduces to six points. But you still have the Eight-Point Circle.
To summarize, the Eight-Point Circle for quadrilateral CABHC has reduced to a six-point circle. Those six points are P, T, R, U, P'=R', T'=U'.
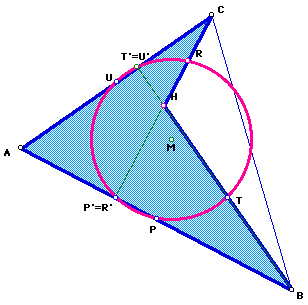
If we compare, the last figure with the previous two, you will notice that there were no new points that appeared on the circle. We began with the eight-point circle corresponding to quadrilateral ABCHA; then proceeded to work with the eight-point circle corresponding to quadrilateral BCAHB; lastly proceeded to work with the eight-point circle corresponding to quadrilateral CABHC. It would make sense that we should have 24 points on our circle. However, each eight-point circle for each of the quadrilaterals corresponded to only six points. Thus, it would make sense that we should have 18 points on our circle. As we have shown geometrically, this is not the case. We have only NINE points on the circle. Those nine points are P, Q, R, S, T, U, P'=R', Q'=S', T'=U'.
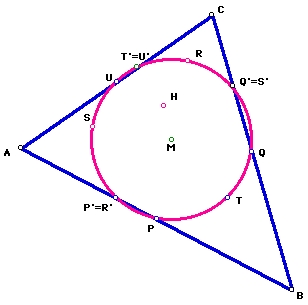
In summary, the common-eight point circle of the quadrilaterals, about the mean center of A, B, C, H, is the NINE-POINT CIRCLE of the triangle.
Amazingly enough, we have shown a beautiful geometric and mathematical relationship between the historically shaded Eight-Point Circle and the geometrically pervasive Nine-Point Circle.
References
Brand, L. "The Eight-Point Circle and the Nine-Point Circle." American Mathematical Monthly 51, 84-85, 1944.
Return to learn more about the Nine-Point Circle