Existence of the Nine-Point Circle: A Geometrical Proof |
I could be bounded in a nutshell and count myself a king of infinite space. William Shakespeare (Hamlet, Act II, Scene 2) |
This geometrical proof is posed as a problem 15 on page 12 in College Geometry: A Discovery Approach by David Kay (1994) and serves as the outline for the proof.
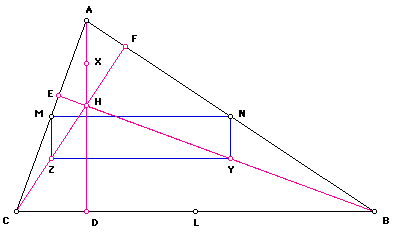
Observe from the following figure that Triangle ABC is a given triangle; L, M, and N are midpoints of the sides; D, E, and F are the feet of the altitudes on the sides; H is the orthocenter; and X, Y, and Z are the midpoints of segments AH, BH, and CH, respectively. Note the quadrilateral MNYZ drawn in the figure.

We have triangle ABC where MN bisects AB and AC. We know MN will be parallel to BC since we have the theorem that states,
If a line bisects one side of a triangle and also bisects the other side, then the line is parallel to the third side.
By a similar argument, ZY is parallel to CB.
We know MN // BC and BC // ZY. By transitivity, MN // ZY. We also have quadrilateral MNYZ. Therefore, MNYZ is a parallelogram.
Next, we can show that NY // AD. Since triangle ADB is a right triangle and N is the midpoint of AB, construct the line NT, with Y being on segment NT.
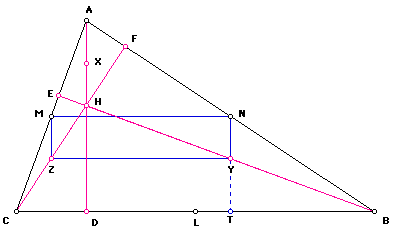
Using the previously mentioned theorem,
If a line bisects one side of a triangle and also bisects the other side, then the line is parallel to the third side,
we have NT // AD; thus NY // AD.
In a similar fashion, AD // MZ. Therefore, by transitivity, NY // MZ.
Now we have quadrilateral MNYZ where both of the opposite sides are parallel to each other and AD is perpendicular to BC is perpendicular to ZY is perpendicular to MN. Thus, all of the angles in parallelogram MNYZ are right implying MNYZ is a rectangle.
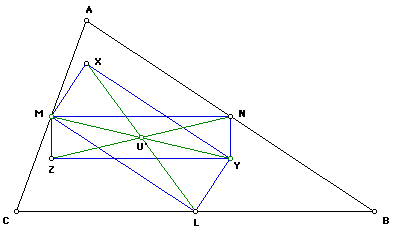
In a similar manner, following the same procedure above, we can show that quadrilateral XYLM is a rectangle.
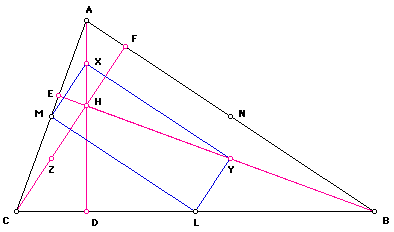
Next, we want to show that U = U'.
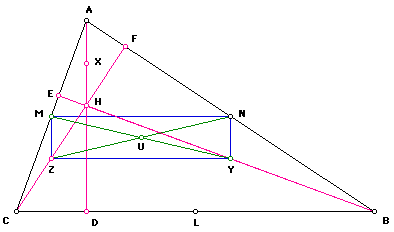
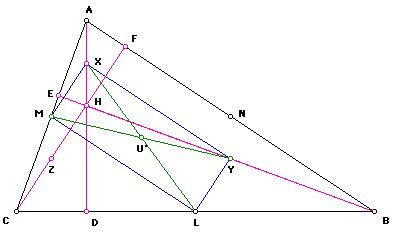
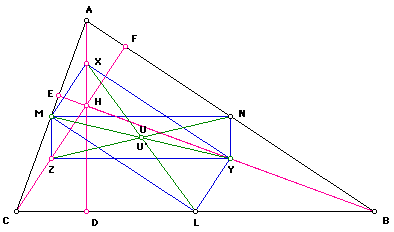
In the rectangle MNYZ, the diagonals MY and NZ intersect at U. Since MNYZ is a rectangle, the diagonals bisect each other and are congruent to each other. So MY=NZ. Consequently, MU=UY=ZU=UN.
In the same manner, the rectangle XYLM, the diagonals MY and XL intersect at U'. Since XYLM is a rectangle, the diagonals bisect each other and are congruent to each other. So MY=XL. Consequently, MU'=U'Y=XU'=U'L.
We know MY = NZ and MY = XL. We can conclude that NZ = XL. Since NZ = XL, and they intersect at both points U and U' in rectangle XYLM, we can conclude that U = U'.
Since MNYZ and XYLM are rectangles, the following is implied (respectively):
MU=UY=ZU=UN
MU'=U'Y=XU'=U'L.
Since we have shown that U=U', substitution gives
MU'=U'Y=ZU'=U'N
and we already know
MU'=U'Y=XU'=U'L.
Consequently,
MU'=U'Y=ZU'=U'N=XU'=U'L.
By definition of a circle,
MU'=U'Y=ZU'=U'N=XU'=U'L
are six radii of a circle U'.
Hence, U' is the center of a circle passing through six (out of nine desired). The six points are
L, M, N, X, Y, Z.
The last three points of the nine points we obtain by focusing our attention on triangle DLX.
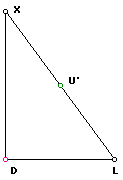
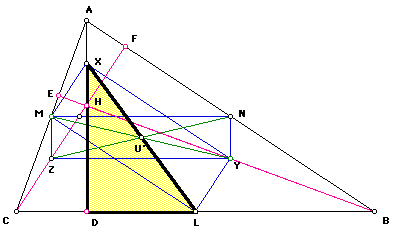
We know XU' = U'L and since XD is perpendicular to DL, triangle DLX is a right triangle .
Based on this given information and the theorem from geometry that states,
The midpoint U' of the hypotenuse of a right triangle DLX is equidistant from the three vertices, D, L, and X, and a circle centered at U' passes through D, L, and X,
U' is the circumcenter of a circle passing through X, D, and L.
From this, we have picked up point D as being on circle U'.
Repeat this same procedure on triangles MEY and FNZ.
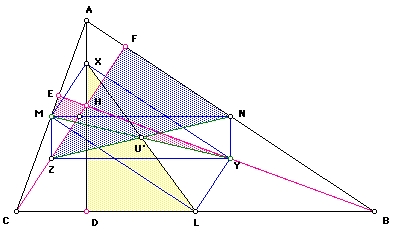
From triangle MEY and triangle FNZ, we pick up points E and F, respectively, to be two more points of the nine point circle.
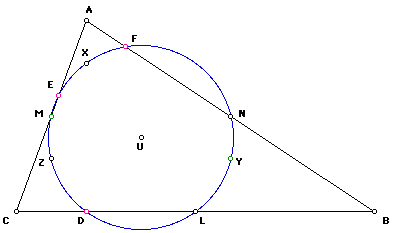
Therefore, U' is the center of the nine point circle that passes through the following nine points:
M, E, X, F, N, Y, L, D, Z.
Thus, we have shown the existence of the nine point circle.
Return to learn more about the Nine Point Circle