
Properties of the Nine-Point Circle and the Nine-Point Center |
What are we to think of the question: Is Euclidean Geometry true? It has no meaning. We might as well ask... if Cartesian coordinates are true and polar coordinates false. One geometry cannot be more true than another; it can only be more convenient.
H. Poincare (1854-1912)
(Science and Hypothesis, New York, 1952)
The Nine-Point Circle of Triangle ABC with orthocenter H passes through the midpoints L, M, and N of the three sides, the feet of the altitudes D, E, and F to those sides, and the Euler Points X, Y, and Z, which are the midpoints of the segments AH, BH, and CH, respectively.

For a proof of the existence of the Nine-Point Circle, click here.
The Nine-Point Center U lies on the Euler Line of Triangle ABC. The Euler line is the line passing through the orthocenter H, the circumcenter CC, and the centroid G of a triangle.
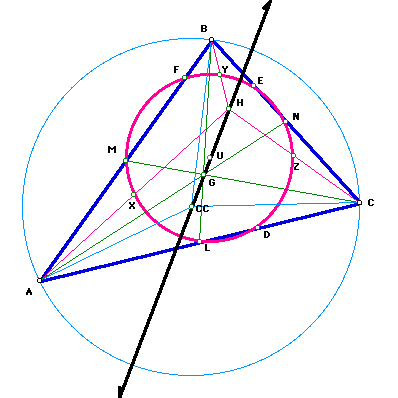

For a GSP Script, click here.
The tangents to the Nine-Point Circle at the midpoints L, M, and N of the sides of the triangle form a triangle, triangle RST, that is similar to the orthic triangle (the triangle DEF). In fact, the sides of this triangle are parallel to those of triangle DEF.
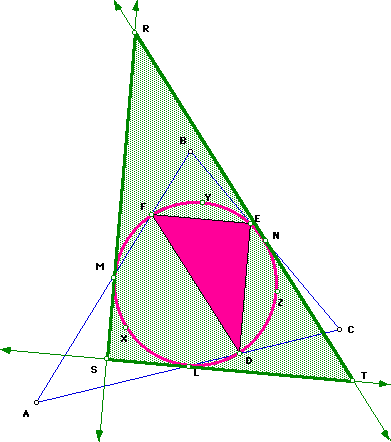
For a GSP Script, click here.
Feuerbach's Theorem
The Nine-Point Circle of a triangle "touches" the incircle and the three excircles.
"touches" implies tangent

For an extensive listing of 20 additional properties about the nine point circle, see the following reference, specifically pages 53-56:
MacKay, J. S. (1892). History of the Nine Point Circle. Proceedings of the Edinburgh Mathematical Society, (11). pages 19-61.
References
Kay, D. (1994). College Geometry: A Discovery Approach. HarperCollins College Publishers: New York.
Return to learn more about the Nine-Point Circle