WRITE-UP 1
Investigating equations in the form of
CASE 1:
n=even positive integer
Consider the following equations of the form ![]() , where n is an even
positive integer, and their graphs:
, where n is an even
positive integer, and their graphs:
![]()
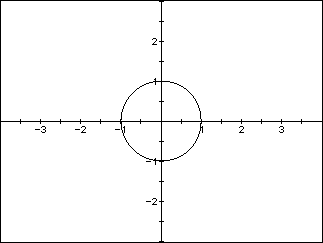
![]()
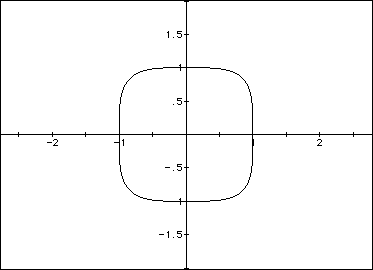
Notice when the indices changed from 2 to 4, the corners have become
sharper and more squared off. If we continue this when n = 6, we notice
the corners becoming even more square like and less rounded.
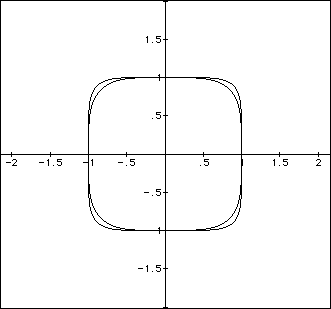
If this pattern continues, we would expect for the equation ![]() that
the corners would be sharper and the graph would look similar to that of
a square.
that
the corners would be sharper and the graph would look similar to that of
a square.
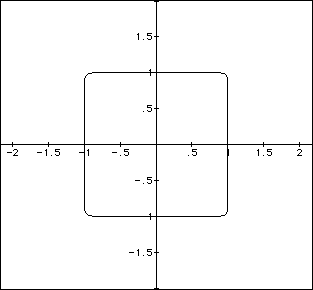
This leads to an interesting question: Do we conclude as n gets larger
the corners will eventually square off and the graph of the equation will
become a square? Consider the graph of ![]() .
.
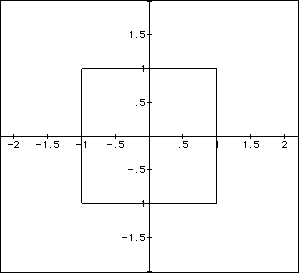
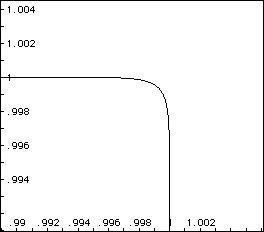
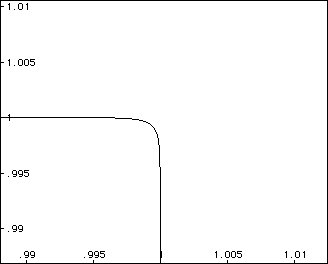
The graph suggests that of a square. We can zoom in on one of the corners
to uncover the true nature of the corners. Magnifying the corner allows
one to verify that indeed the corners are still rounded and not square like
as the graph had originally suggested.
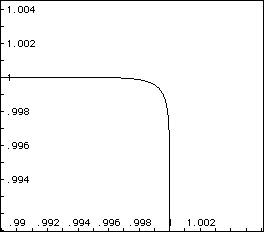
We can continue this process for n being very large only to conclude
the same results:
As n continues to grow as an even positive integer, the graph may suggest
a square. Yet, further analysis verifies that the corners will always be
rounded.
Consider the general equation : ![]() .
.
If we let n=any positive even integer and x = y =1, the equation does not
hold true.
Therefore, (1,1) can never be a solution to the equation. Thus the graph will never represent that of a square.
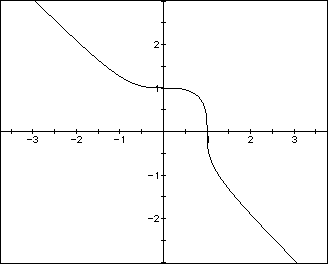
Consider the following equations of the form ![]() , where n is an odd
positive integer, and their graphs:
, where n is an odd
positive integer, and their graphs:
![]()
![]()
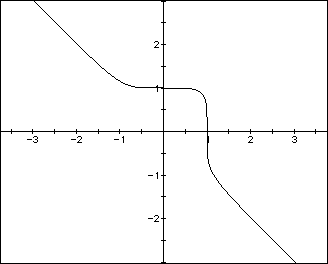
Similarly to Case 1, notice as n increases the graph is becoming sharper
and square-like at the corners.
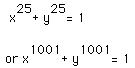
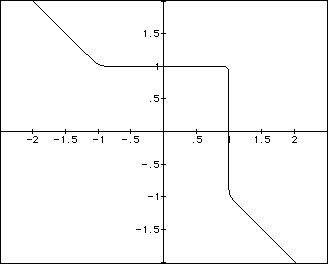
As in Case 1, to obtain a half-square, the points (-1,1), (1,1), and (1,-1) would have to be solutions to the equation under investigation. Indeed, they are NOT solutions. Therefore, we can continue to increase n as large as possible, regardless of n being odd or even, and the graph may look as if it is transforming into squares or half-squares. In reality, however, when the graph is magnified, the corners are curved, not forming 90-degree angles.