Write-up #10

Question #3

Parametric Curves

If x and y are given funtions

x=f(t)
y=g(t)

over an interval of t values, the the set of points (f(t), g(t)) defined by these equations is a parametric curve in the coordinate plane. The equations are parametric equations for the curve, and we say the curve has been parametrized. The variable t is the parameter of the curve, and its domain I = [a,b] = [tMin, tMax] is the parameter interval. The point (f(a), g(a)) is the initial point of the curve, and (f(b), g(b)) is the terminal point of the curve.

Consider

x = a cos(t)
y = b sin(t)

for for various values of a and b.

We want to investigate the curve when a < b, a= b, and a> b.
Our exploration begins when a < b.


Consider the graph when a=1 and b = 3. The associated equations are

x = 1 cos(t)
y = 3 sin(t)

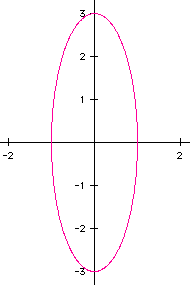
The graph is an ELLIPSE crossing the x axis at -1 and 1 and the y axis at -3 and 3.

What might you expect when a = -4 and b = -2?

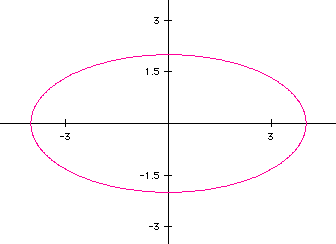
As expected, the ellipse intercepts the x axis at -4 and 4 and the yaxis at -2 and 2. Notice, however, the ellipse has the x axis as it's major axis whereas in the previous example the major axis was the y axis. Recall from your study of the conic sections , particularly the ellipse,

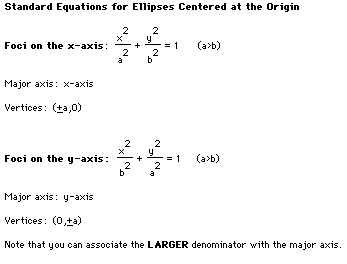
that you can associate with the major axis. This translates into our knowledge of parametric equations.

For example, we have our beginning equations

If we divide each side of the equations by a and b respectively, we obtain the following:

.

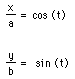Now if we square both sides of each equation and add each side of the equations,

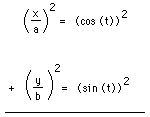
we obtain the following:

.

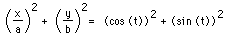This equation can be simplified further using the trigonometric identity, .

Thus the equation becomes

which is the equation for an ellipse.

Recall from above that when a<b, we get two different cases where the major axis can be the x-axis or y-axis. What case produces the x-axis as its major axis? and y-axis as its major axis?

Let's try several more examples to see if there is a pattern. Remember a<b.

Consider the two cases:
a=-4 and b=1 (pink)
a=-4 and b=9 (torquoise). The graph suggest the following ellipses:

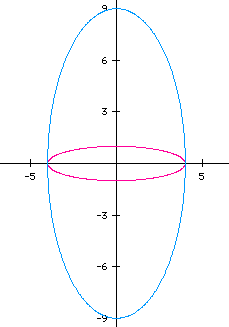
In both cases, a<b. The key to identifying the major axis of the ellipse is looking at the absolute value of a and b. Notiçe when |a|>|b|, the x-axis is the major axis. When |a|<|b| the y-axis is the major axis.

Now, consider the graph when a=-3 and b=3.

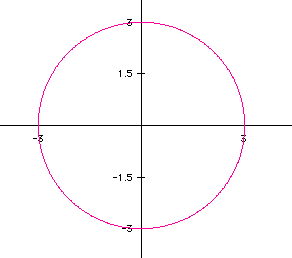
As expected, the ellipse crosses the x-axis at -3 and 3 and the y-axis at - 3 and 3. Yet, in this case we get a circle which can also be considered a "special case" of an ellipse.
Notice .
If we consider our equations for an ellipse, since , our ellipse will be a circle.
Furthermore, when |a|=|b|, the equation will be an ellipse.

What if we consider the case where either a or b is equal to zero?

Let a=­p;2 and b=0 , equations are

x = -2 cos (t)
y = 0 sin (t)

where .

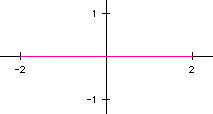
The graph is a straight line whose endpoints are -2 and 2. For every t, the output is an ordered pair (x,y) which in this case is (-2 cos(t),0). Thus, a line segment is expected.

Another perspective to answer the question, "What happens if either a or b is equal to zero?" is to investigate the parametric equations

x = a cos (t)
y = b sin (t)

and their respective graphs as b tends to zero and a is any number.

Letting a=-2 and b tend to zero, consider the following graph where

b=1/2 (pink)
b=1/4 (turquoise)
b=1/8 (green)
b=1/16 (red)
b=1/32 (royal blue)

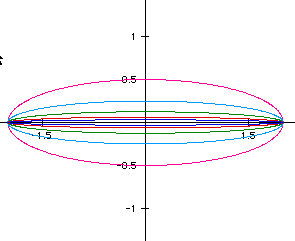
Notice, as b tends to zero, the ellipse becomes thinner and thinner. If you let b=0, the ellipse will become a segment.

Our next journey investigates when a = b.


Consider when a=b=3, we have the equations

x=3 cos(t)
y=3 sin(t)

and the graph

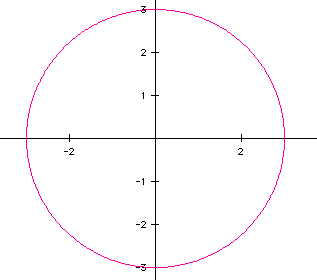
is a CIRCLE whose radius is a=b, in this case a=b=3.  You can also consider this circle as a "special case" of an ellipse where the x- and y-intercepts are the same. Hence, the distance from the origin to each vertice is equal and a circle is formed.

Consider when a=b=-6.

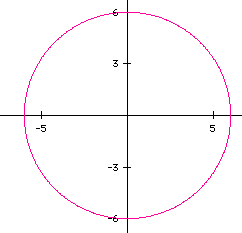
As predicted, the graph is a circle whose radius is |-6 | = 6. Remember, the length of a radius is always positive. Thus, in the parametriç equations

when a=b, the graph will always be a circle with radius=|a|=|b|.

Our last investigation centers around when a>b?

Consider when a=5 and b=3. The associated equations are

x = 5 cos(t)
y = 3 sin(t)

and the graph is as follows:

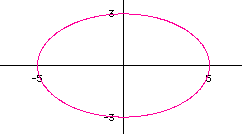
The graph is an ellipse with x-intercepts at and y-intercepts at with |a|>|b|. Using our previous conclusion the graph should have the x-axis as its major axis. This is a true statement.

Consider the case when a=4 and b=-2. The associated equations are

x = 4 cos (t)
y = -2 sin (t)

and the graph is as follows:

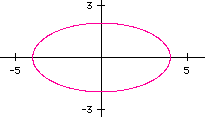
Consider the case when both a and b are both negative and a > b.
Let a=-4 and b=-8. So,

x=-4 cos (t)
y=-8 sin (t)

and the graph (pink) is

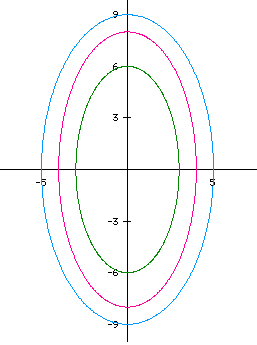
Also, consider several other cases where a=-5 and b=-9 (turquoise) and a=-3 and b=-6 (green).
Notice the y-axis is the major axis. Recall from our previous discussion, when |a| < |b|, the major axis is the y-axis.

Summary

Overall, this investigation explores the connection between parametric equations as it relates to the equation of an ellipse and its associated graph. The assertion that the parametric equations

x = a cos (t)
y = b sin (t)

will always produce an ellipse was shown algebraically. The process involved squaring both sides of each equation, adding the equations together, and using a common trigonometric identity. This proved essential in making the connection. We also explored different cases involving a<b, a=b, and a>b. Several conclusions drawn were when

a) |a| > |b|, the major axis lies on the x-axis
b) |a| < |b|, the major axis lies on the y-axis
c) a=b, the ellipse will be a circle.

This exploration would prove most beneficial to a secondary mathematics course when studying ellipses. Why? Parametric equations are not dealt with heavily in the traditional curriculum. This investigation could be used after ellipses have been discussed and in conjunction with an introduction into the concept of parametric equations. Hence, students can sample a taste of an entirely new concept, parametric equations, along with a connection to an old concept, ellipses. This mathematical activity allows students a new perspective on ellipses providing them with a different way to see ellipses. As a mathematics educator, one of my goals is to provide students with alternative ways of viewing a mathematical concept. Furthermore, another goal is to provide opportunities for students to make connections between mathematics concepts themselves. This exploration fulfills both goals. In addition, the use of technology is utilized. The technology used provides students with new mathematical learning experiences while at the same time the learning is enhanced using technology.

Return