

and to overlay several graphs of
for different values of a, b, or c as the other two are held constant.
From these graphs discussion of the patterns for the roots of
can be followed. For example, if we set
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following
picture is obtained.
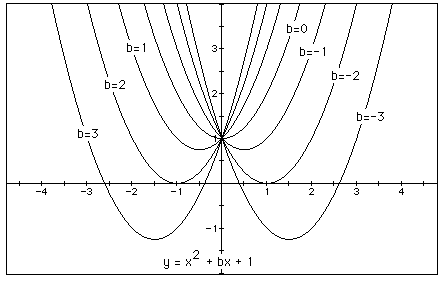
We can discuss the "movement" of a parabola as b is
changed.
The parabola always passes through the same point on the y-axis ( the point
(0,1) with this equation).
For b < -2, the parabola will intersect the x-axis in two points with
positive x values (i.e. the original equation will have two real roots,
both positive).
For b = -2, the parabola is tangent to the x-axis and so the original equation
has one real and positive root at the point of tangency.
For -2 < b < 2, the parabola does not intersect the x-axis -- the
original equation has no real roots.
Similarly for b = 2 , the parabola is tangent to the x-axis (one real negative
root).
For b > 2, the parabola intersects the x-axis twice to show two negative
real roots for each b.
To summarize:
The nature of the roots for the equation
as b varies from -3, -2, -1, 0, 1, 2, 3 are as follows:
We can investigate
- b < -2 ---------------2 positive real roots
- b = -2 ---------------1 positive real root
- -2 < b< 2 -----------no real roots
- b = 2-----------------1 negative real root
- b > 2 ----------------2 negative real roots
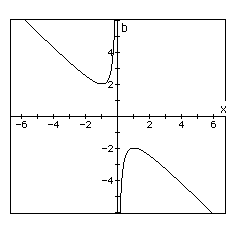
Now graph this relation in the xb plane. We get the following graph.
If we take any particular value of b, say b = 3, and overlay this equation
on the graph we add a line parallel to the x-axis. If it intersects the
curve in the xb plane the intersection points correspond to the roots of
the original equation for that value of b. We have the following graph.
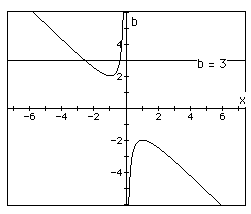
For each value of b we select, we get a horizontal line. It is clear
on a single graph that we get two negative real roots of the original equation
when b > 2, one negative real root when b = 2, no real roots for -2 <
b < 2, one positive real root when b = -2, and two positive real roots
when b < -2.
The method of graphing the quadratic in the xb plane is rather helpful to
students who may have difficulty identifying the nature of the roots in
the traditional xy plane. It lessens the confusion for students especially
in the case when -2 < b < 2. Notice the graph when b = -1 and b =1.
Clearly, students can easily conclude that since b=-1 and b=1 do not cross
the graph, there are no real roots for the equation.
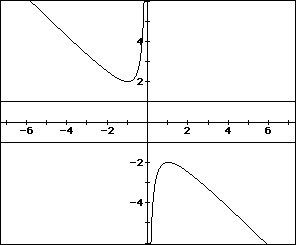
Consider the case when c = - 1 rather than + 1.
First, consider the graph of
in the traditional xy plane and let b= -3, -2, -1, 0, 1, 2, 3. The graph
looks similar to the original equation when c = 1.
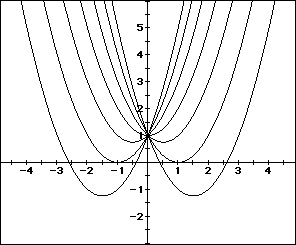
From the graph, when b=0, the equation will have one real root. Otherwise,
the equation will have 2 real roots, one positive and one negative.
Now consider the graph of
in the non-traditional xb plane.
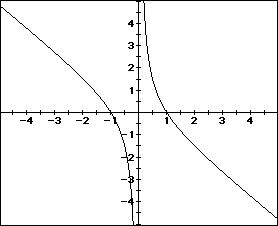
Graphing the equation in the xb plane allows the student to see the nature
of the roots faster and easier as compared to the traditional xy plane.
At a quick glance students know that the equation will always have two real
roots, one positive and one negative. Using the xy plane, students have
to analyze the graph in much more detail as compared to the graph in the
xb plane. Students can also verify the nature of the roots by using the
discriminant. In this case the discriminant is ![]() which is always greater
than zero. Thus the equation has two real roots as expected from the graph
in the xy and ab plane.
which is always greater
than zero. Thus the equation has two real roots as expected from the graph
in the xy and ab plane.
Now consider when b is constant and c varies.
In the following example, the equation
is considered.
Since c is varying in this equation, we will look at the graph in the xc
plane to determine the nature of the roots.
If the equation is graphed in the xc plane, it is easy to see that the curve
will be a parabola.
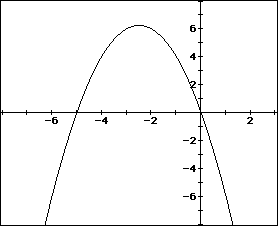
For each value of c considered, its graph will be a line crossing the
parabola in either 0, 1, or 2 points -- the intersections being at the roots
of the original equation at that value of c. To reiterate, students can
easily and quickly glean the roots of the equation using this method where
the equation is graphed in a non-traditional approach; that is the xc plane.
For example, the graph of c = 1 is shown.
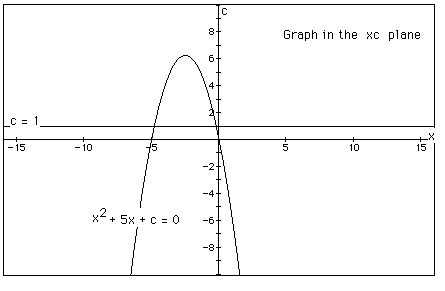
The equation
will have two negative roots -- approximately -0.2 and -4.8.
Now it might be of interest to determine when the equation will have only
one real root.
There is one value of c where the equation will have only 1 real root; that
is at c = 6.25. This information can be easily conjectured and verified
from the graph when c = 6.25.
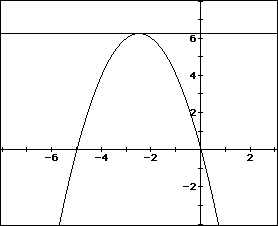
Furthermore, for c > 6.25 the equation will have no real roots.
When c < 6.25 the equation will have two roots. More specifically, the
roots will both be negative for 0 < c < 6.25, one negative and one
0 when c = 0, and one negative and one positive when c < 0.
For final proof that this "different" method has merit, consider
the graph of the equation at hand,
in the traditional xy plane.
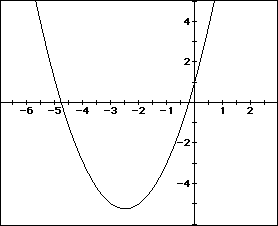
To determine what values of x produce the three cases of possible roots;
that is, 0, 1, or 2 roots, would take a considerable amount of time changing
the values of c. Also, picking a large amount of values for c and then overlaying
their graphs would produce some insight.
For example, notice the graph when c = 1 and c =8.
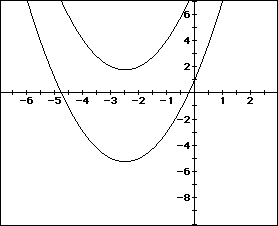
Students would have to continue picking values of c and then narrowing
down the values of c until they find the value of c that has no real roots
of the equation
namely, c=6.25, in this example.
Students may also point out at this step it would be easier to use the discriminant
to find the value of c that gives no real roots of the equation.
On a final note, it is important to stress that this "different"
method should not altogether replace the other method that uses the traditional
xy plane. Pedagogically speaking however, it is always good to show students
alternate ways of approaching a problem or task. This article is simply
another way of approaching the task of teaching students how to determine
the nature of the roots as well as the roots of a quadratic.