What is a tangent to a circle?
The word tangent comes from the Latin word meaning "touching."
This notion of touching is used in the geometrical meaning of tangent. Think
of a wheel (circle) as tangent to a ramp (a line) as it rolls up or down
the ramp. The wheel and the ramp are thought to have one point in common
in a given plane. This is called the point of tangency.

A tangent to a circle is a line in the plane of a circle which
intersects the circle in exactly one point. This point is called the point
of tangency.
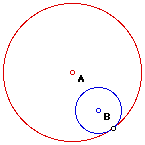
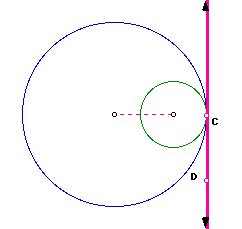
Two circles in the same plane are externally tangent if they intersect
in exactly one point and their intersection of their interiors is empty.
Next, we want to discuss the cases when you have two circles and their
respective common external and internal tangents.
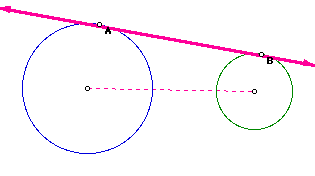
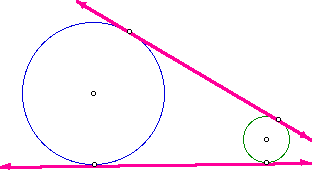
A tangent of two circles is a common external tangent if the intersection
of the tangent and the line segment joining the centers is empty.
For example, line AB and line CD are common external tangents.
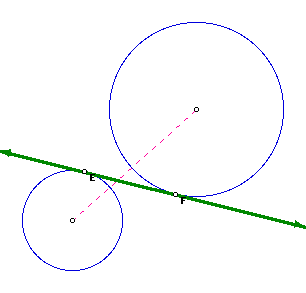
A tangent of two circles is a common internal tangent if the intersection
of the tangent and the line segment joining the centers is not empty.
For example, line EF and line GH are common internal tangents.
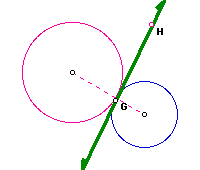
How many common external and internal tangents will the following sets of
circles have?
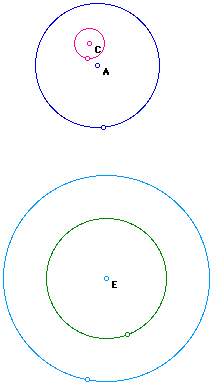
Your answer should be NONE. Since the circles are not internally or externally tangent to begin with, Circles A and C and concentric circles E will not have any common internal or external tangents.
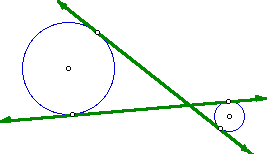
Click here for a demonstration
for all of the possible EXTERNAL TANGENT cases for two given circles.
Scripts have been made for common external and internal tangents.
Click here for common external tangent script.
Click here for common internal tangent
script.