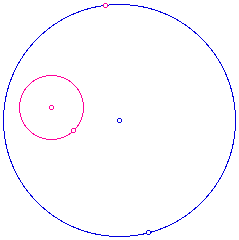

The construction can be completed by the following
a. Construct a line through the center of the circle with the designated
point of tangency.
b. Construct a circle of the same radius as the second of the given circles
with the designated point as center.
c. The intersection of the line and circle will allow construction of the
base of an isosceles triangle.
d. Drop a perpendicular bisector through the base of the isosceles triangle.
e. The intersection of the perpendicular bisector and the line drawn through
the point of tangency will be the center of the desired circle.
f. Draw the desired circle.
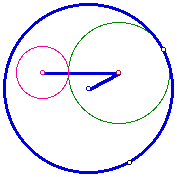
The following picture shows the completed construction
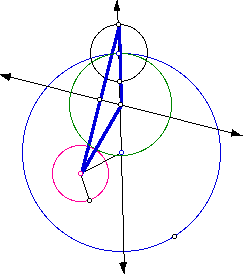
Click here for a GSP script for construction
of the tangent circles.
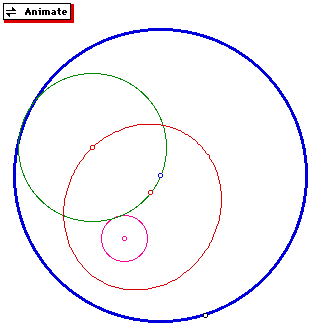
Given the construction, consider the locus of the center of all such circles
tangent to the two given circles. With GSP we can animate around the circle
and trace the locus of the center.
Click here for an animation around the
circle while tracing the locus of the center (point).
Click here for an animation around the
circle while tracing the locus of the center (line).
What did you discover as the locus (red) of the center was being traced?

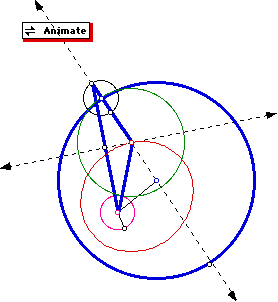
Most interesting, the locus of the centers of the tangent circles is
an ellipse.
Notice if the center of the constructed circle is connected by segments
to the centers of the two given circles, the sum of the segments is the
same as the sum of the radii of the two given circles. This sum is a constant.
Therefore, the locus of the centers of the tangent circles is an ellipse
with foci at the centers of the given circles.
Students have a difficult time with the conic sections. This investigation
would be useful to help students understand the concept of an ellipse. Once
students have been introduced to the definition of an ellipse, this exploration
would further enhance and build on their concept of an ellipse.
It is also a great investigation into other topics used in the geometry
curriculum. For example, students would have to recollect the properties
and theorems associated with isosceles triangles and perpendicular bisectors.
In addition, this exploration stresses the connections between geometrical
concepts . Students often categorize geometrical concepts. They see mathematical
concepts as being separate from each other. With the use of GSP, this investigation
gives students opportunities to see the underlying relationships between
many of the geometrical concepts that would be difficult if not for GSP.