PEDAL TRIANGLES
What If?


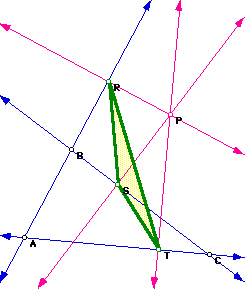
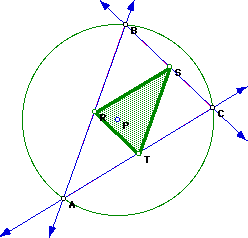
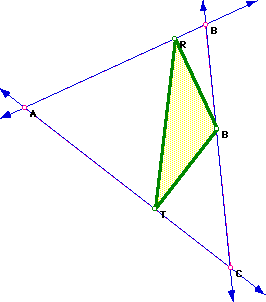
Let triangle ABC be any triangle. If P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) from P where points R, S, and T are the intersections is called the Pedal Triangle.

Triangle RST is the Pedal Triangle for Pedal Point P.

Click here for a GSP script to construct a pedal triangle where P is any point in the plane of ABC.

Click here for a GSP animation for various locations of point P.


WHAT IF...?

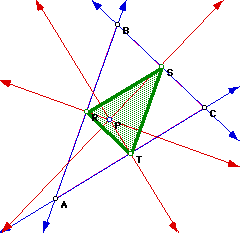
Next we want to investigate different scenarios for point P depending on the location of P.

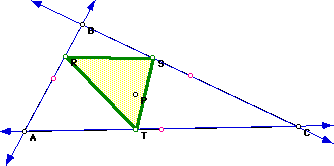
What if ... pedal point P is the centroid of triangle ABC?

Recall the centroid of a triangle is the common intersection of the three medians.

Click here for a GSP animation for various shapes of triangle ABC.

What did you notice?

What if ... pedal point P is the incenter of triangle ABC?

Recall the incenter of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angles lies on the angle bisector, then the incenter must be on the angle bisector of each angle of the triangle.
The incenter is the center of the incircle, the inscribed circle of the triangle.

First, construct the incenter and the incircle for triangle ABC.


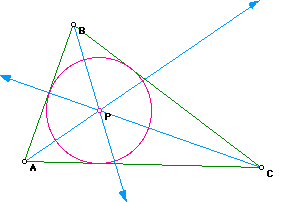
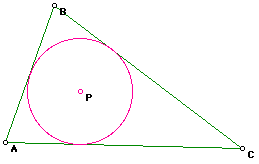
What do you expect when the incenter P becomes the pedal point for triangle ABC?

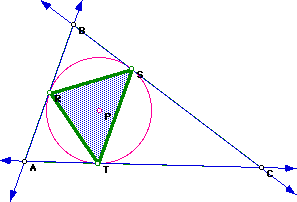
The vertices of the Pedal Triangle RST lie on the incircle of triangle ABC. WHY?
The pedal point P is constructed by dropping perpendicular lines from P to each side of triangle ABC. Then the Pedal Triangle is formed. Its vertices, R, S, and T are the points of intersection with each side of triangle ABC. When P is the incenter, the incircle is also constructed by dropping perpendicular lines from P to each side of the triangle ABC. Hence, when P plays both roles, the incenter and the pedal point of triangle ABC, the construction is the same for the incircle and the pedal triangle, RST.

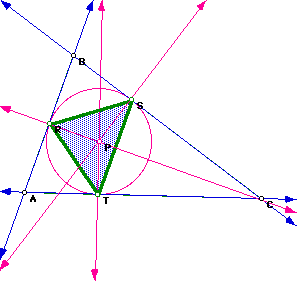
Does this hold for various shapes of triangle ABC?
Click here for a GSP animation to investigate.

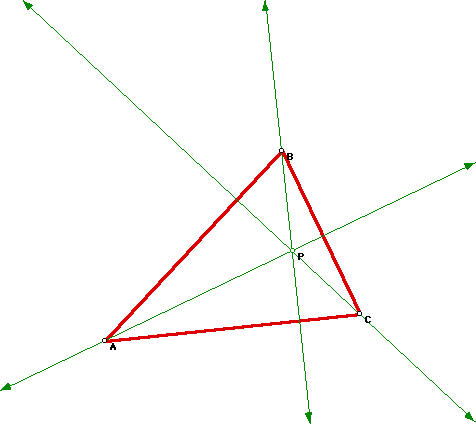
What if ... pedal point P is the orthocenter of triangle ABC?

Recall the orthocenter of a triangle is the common point of intersection of the three altitudes.

The orthic triangle is the triangle connecting the feet of the altitudes.

Consider what happens when P is the orthocenter and the pedal point for triangle ABC.

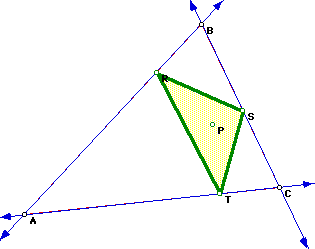
As expected, the orthic triangle is also the pedal triangle RST.

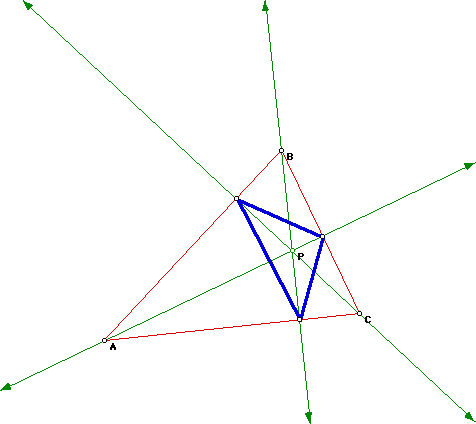
What if the orthocenter is outside of triangle ABC? Does this conjecture still hold true?
YES.

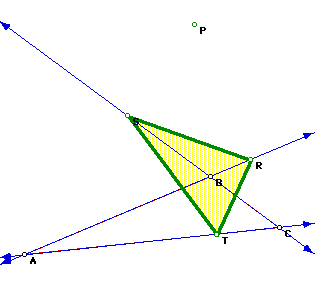
Click here for a GSP animation for various shapes of triangle ABC and its effect on P and triangle RST.

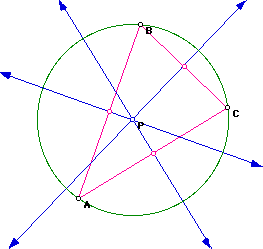
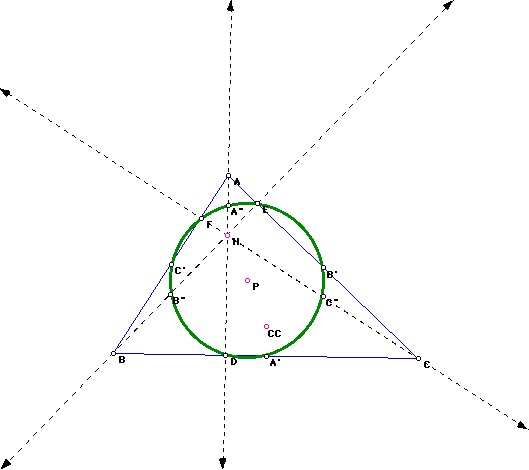
What if ... pedal point P is the circumcenter of triangle ABC?

Recall the circumcenter of a triangle is the point in the plane equidistant from the three vertices of the triangle; that is, the perpendicular bisectors of the three sides of a triangle all pass through the circumcenter. It is the center of the circumcircle, the circumscribed circle of the triangle.

From the construction of the circumcenter, we can construct the medial triangle. The medial triangle is the triangle formed by connecting the three midpoints of the sides of the triangle.

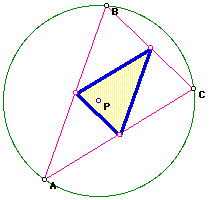
What if we construct the pedal triangle using the circumcenter as the pedal point?

The pedal triangle RST is also the orthic triangle for triangle ABC. This can be examined by investigating the construction of the pedal triangle RST.

When P is outside of triangle ABC, is the pedal triangle still the orthic triangle?

Click here for a GSP animation for changes in pedal point P and pedal triangle RST as triangle ABC changes shape and size.

What if ... pedal point P is the center of the nine point circle for triangle ABC?

Recall the Nine-Point Circle for any triangle is the circle that contains the midpoints of the three sides, the midpoints of the lines joining the orthocenter to the three vertices, and the feet of the three altitudes. These nine points all lie on the nine point circle also referred to as the "Feuerbach circle."
This circle is the first really exciting one to appear in any course on elementary geometry.
Daniel Pedoe [1910- ]

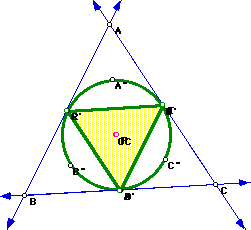
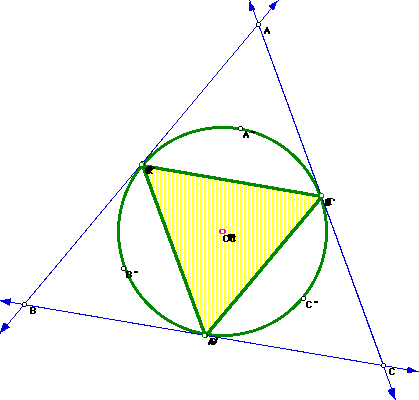
Next construct the pedal triangle RST using the center, P, of the nine point circle for triangle ABC as the pedal point.

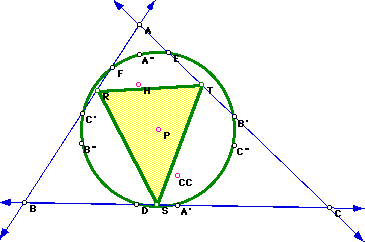
Notice the Pedal Triangle RST will lie on the nine point circle when the circumcenter, CC, orthocenter, H, and the pedal point, P, all are the same point; that is, when the circumcenter and the orthocenter become the center of the nine point circle also known as P.

Here are a few examples:






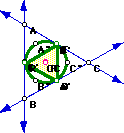
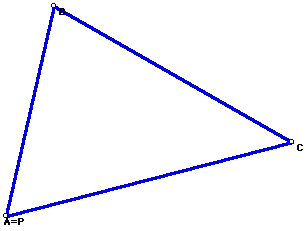
What if ... pedal point P is on the side of triangle ABC?

Begin by constructing triangle ABC with point P on the side of triangle ABC.

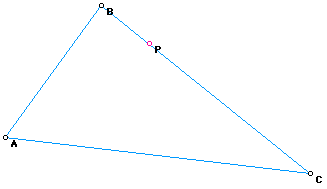
Next construct the pedal triangle RST using P as the pedal point where P is on the triangle ABC.

What do you discover?

When a pedal point, P, is located on the side of triangle ABC, P will always be a vertex on the pedal triangle RST.

What if ... pedal point P is one of the vertices of triangle ABC?

Construct triangle ABC with pedal point P as vertex A.

This construction was not possible using the script for the general construction of a triangle ABC. The script needs three vertices and a point P that cannot be a vertex.

Think about this...

Given triangle ABC with pedal point P as vertex A.

Next, follow the steps to constructing the pedal triangle RST.

First, construct the perpendicular from point P to side BC of triangle ABC.

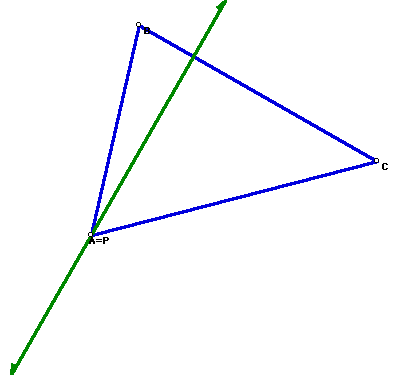
Next, construct the perpendicular from point P to sideAB of triangle ABC.
You notice something very interesting. This step CANNOT be done. It is not possible.

Try this...

Try constructing the perpendicular from point P to side AC of triangle ABC. This also is not possible.

Therefore, when the pedal point of a triangle is also a vertex of the triangle, the pedal triangle cannot be constructed.


Concluding Remarks:

This activity was the most interesting and insightful of all the GSP write-ups. This activity connected all of the geometric concepts that we have studied thus far. It was an ideal experience that tied together everything that we have been working on. To complete this write-up, an understanding of all the basic geometrical concepts such as centroid, incenter, incircle, orthocenter, orthic triangle, circumcenter, circumcircle, and the nine-point circle was necessary. This would be a great geometry activity for an overall review and summation of the main geometrical concepts previously mentioned. The connection between the nine-point circle and the pedal point was my favorite.

Return