

Write-up 10 deals with parametric curves. A parametric curve in the plane is a pair of functions x=f(t) and y= g(t) where two continuous functions defined order pairs (x,y).
Problem: Investigate each of the following for zero less than or equal to t and t is less than or equal to two pi. Describe each when a=b, a<b, and a>b. The parametric equations we are looking at are the following.
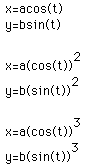
First I looked at the graphs of degree one. Which is the first two equations above.
I. The following graph shows when a=b, we will always get a circle with the radius of a=b. When -a=-b we get the absolute value and therefore, get the same graph.
II. When a>b, we get a graph of an ellipse with the major axis being the x-axis such that the length is 2a and the minor axis is the y-axis what is equal to b.
III. When a<b, we get a graph of an ellipse, but this time the major axis is the y-axis which is 2b. And the minor axis is the x-axis which is the length of a.
The next set of graphs that I looked at were of degree 2.
I. When a=b, we get a graph of a line segment with the endpoints being a=b. This holds true even when -a=-b. The only difference is the quadrant that you are in. When a=b, you are in the first quadrant and when -a=-b, you are in the third quadrant.
Conclusion: Therefore, whether a>b or a<b, you will always get a line segment with the endpoints being a and b. The only difference is what quadrant you are in.
The last set of parametric equations that I looked were of degree three.
I. When a=b, we get an "inverted" ellipse with the length equal to a and b.
II. When a>b, it stretches out the x-axis of the length of a.
III. When a<b, it stretches out the y-axis the length of b.
Generalization:
I. Even Powers:
For even powers, your graph will be a line segment with a and b as endpoints, but as the power increases for even powers the graph still has endpoints of a and b. The only difference is that as the even power increases in multiples of two, the graph appears to become asymptotic to the x and y axis.
II. Odd Powers:
For odd powers, the endpoints will still be the value of a and b. The graph of odd powers will be our picture of an "inverted" ellipse with it becoming more asymptotic to the x and y axis.
If I was doing this with my students the following is what I would do.
Step I: Graph the equations x=a(cos(t)) and y=b(sin(t)). For your first exploration let a and b equal each other.
a.Use a set of negative numbers for a and b.
b. Use a set of positive numbers for a and b.
What observation can you make? How would you describe the shape of the parametric equations to someone who does not know what a parametric equation is?
Step II: Graph the equations x=a(cos(t)) and y=b(sin(t)). Now let graph the two parametric equations, but this time let a>b.
a. negative values?
b. positive values?
What observations can you make about these graphs. What are some observations you can make from Step I and II?
Step III: Graph the equations x=a(cos(t)) and y=b(sin(t)). Now let a<b.
a. negative values?
b. positive values?
What observations can you make about these set of graphs? Are they the same, different, or not related at all to the graphs in Steps I and II?
Step IV: Follow the same step as you did for Steps I, II, and III. Now use x=a(cos(t))^2 and y=b(cos(t))^2. Answer the same questions as above.
Step V: Follow the same steps as in Steps I, II, and III. This time use the graphs x=a(cos(t))^3 and y=b(sin(t))^3. Answer the same questions as above.
Step VI: What are some generalizations, if any, you can make about increasing the degree without graphing?
Step VII: Write about one other degree for a set of parametric equations. Please have pictures to support your findings.
Step VIII: Please prepare writ-up that contains all of your work and explanations of what you discovered with working with parametric equations.