
Write-up 2

When beginning to work with quadratic equations, we usually
start with quadratic equations in the form of ![]() explore
with different values of a. In the following examples
we will look at positive and negative integer values for a and positive
and negative rational values for a.
explore
with different values of a. In the following examples
we will look at positive and negative integer values for a and positive
and negative rational values for a.
Here we will look at the following equations in order to come up with a hypothesis.
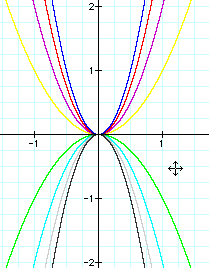
The above picture shows the graphs when a is a positive
or negative integer. The yellow graph that opens upward is the equation
![]() . The rest of the graphs that open upwards are examples
of what happens when we increase the value of a. Here we let a= 1,2,3, and
4.
. The rest of the graphs that open upwards are examples
of what happens when we increase the value of a. Here we let a= 1,2,3, and
4.
The green graph that opens downward is ![]() .
The rest of the graphs are examples of what happens when we
decrease the value of a. Here we let a= -1,-2,-3, and -4. The graph of
.
The rest of the graphs are examples of what happens when we
decrease the value of a. Here we let a= -1,-2,-3, and -4. The graph of ![]() is between the light blue and the dark gray. It is such a
light gray that on here it looks like it is not there.
is between the light blue and the dark gray. It is such a
light gray that on here it looks like it is not there.
From the above we can already make some assumptions. First of all, when a is positive the graph is going to open upward and when the graph is negative it will open downward. Secondly, as we either increase a to be an integer greater than one the graph begins to close up or as I tell my students it is trying to eat the y-axis. Keeping that in mind let us now look at examples when a is a rational number.
I will now look at examples when a is a rational number.
Some examples we will look at is when a= ![]() ,
, ![]() ,
,![]() , and
, and ![]() .
The graphs below are examples when a is
.
The graphs below are examples when a is
equal to the above mentioned values for positive and negative values.
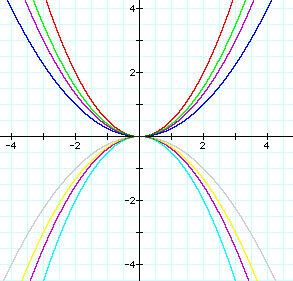
As we can see from the above graphs the opposite occurs when a is a rational number. We can see that the graphs are "pushing" themselves down on the x-axis.
1.Therefore, from are findings we know that when a is a value that is larger than 1, our graph becomes steeper.
2.When the value of a is between 0 and 1, the graph is wider and therefore flattens out towards the x-axis.
3. A conclusion we can make from 1 and 2 is that how steep or wide our graph is depends on the size of a. Whether a is an integer or rational number does not necessarily determine the steepness or wideness of our graph.
4.Whether a is positive or negative determines what way our graph will open. If a is negative then the graph will open downward. If a is positive, the graph will open upward.