

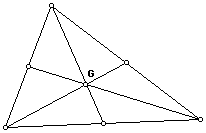
This write-up is exploring the the CENTROID of a triangle. The CENTROID of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. This is demonstrated below.
Click here to see GSP Construction
In the above circle, G is the centroid. I will explore its location for various shapes of triangles.
Right: In the above constructions, you can see that for a right triangle the centroid is always in the center of the triangle. Try and move the endpoints but still keeping one at 90 degrees you will see that the centroid is in the center all the time.
Obtuse: Also with the obtuse triangle the centroid is always in the center. If we were to move any vertex of the triangle we would see that the centroid is always in the center.
Acute: As our findings for the first two investigations the centroid is always in the center of the triangle also.
To see the above explorations click here GSP constructions.
Conclusion: Therefore, the centroid is always in the center and never moves out of any of the vertices of the triangle. Also we see that the ratio of the midpoint to the centroid to the centroid to the opposite vertex from the midpoint is 1/2. And if we switch the ratios and did the segment from the vertex to the centroid over the centroid to the midpoint the ratio would be 2. Finally, I looked at the area of the six triangles that are formed when we construct the centroid. I found that the area of the six triangles constructed area are of equal area.