

In the following investigations, we are asked to construct the orthocenter for triangle ABC. This can be seen below.
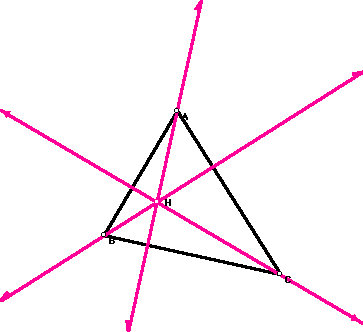
In the above picture, the orthocenter center is marked by the letter H. From this we are asked to create the circumcircle. From the above picture we are then asked to construct the orthocenter and circumcircle for triangles HAC, HCB, and HAB.
A comment on the orthocenters. The orthocenters for triangles HAC, HCB and HAB all ended up being the original vertices of the triangle ABC.
I first began with the orthocenter of triangle ABC as illustrated above. Below is the construction of the circumcircle for triangle ABC.
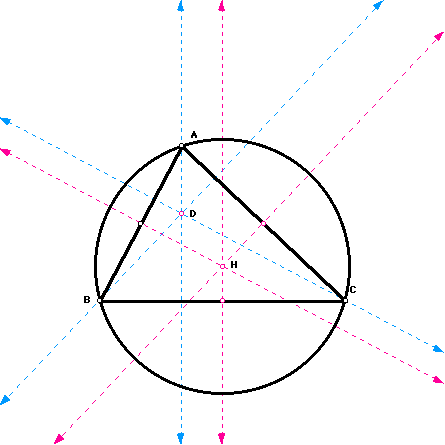
The orthocenter for triangle HAC was the vertex labeled B. Also below is the circumcircle for triangle HAC. This is illustrated below.
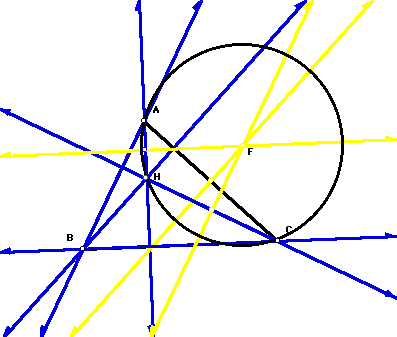
The orthocenter for triangle HCB was the vertex labeled A. Also the circumcircle for triangle HCB is illustrated below.
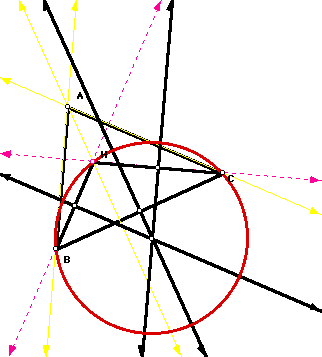
And finally the orthocenter for triangle HAB was the vertex labeled C. Also the circumcircle is illustrated below for triangle HAB. See illustration below.
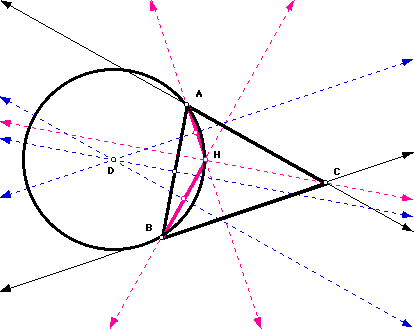
General Comments:
A. The orthocenter of each orthic triangle is the vertex of the original that is not included in the orthic triangle.
B. The circumcircles intersect at the orthocenter of the original triangle ABC.
C. When triangle ABC is a right triangle, the circumcenter of triangle ABC will be concurrent with the circumcenter of the orthic triangle that lies on the hypotenuse.
D. When triangle ABC is an equilateral triangle the circumcenters of the orthic triangles lie on the circumcircle of triangle ABC.
Below is the construction for the incircle, three excircles and the nine point circle for the original triangle ABC.
Click here to see constructions for all the above mentioned.
Conjecture:
You can see from the above construction that the nine point circle is tangent to to the incircle and the three excircles.