

In this write-up, I will be exploring different sets of linear functions and performing the operations of addition, multiplication, division, and composition.In the following explorations, I will be showing how I would implement this into my classroom.
In order to complete the following activity, the students will be using Graphing Calculator.
The following exploration is what they will be expected to do.
i.) h(x) = f(x) + g(x)
ii.) h(x) = f(x)*g(x)
iii.) h(x) = f(x)/g(x)
iv.) h(x) = f(g(x))
I would create the exploration into steps to help them have some type of organization in their exploration of linear functions.
The first step would be to pick two totally different linear functions and to perform the above operations. I would explain that they can pick any linear functions that they want, and therefore it is possible for everyone in the class to have different answers.
say they picked f(x)
= ![]() and g(x) =
and g(x) = ![]()
They would be expected to take the above functions and do steps i - iv. I would like along with this to see some graphs and a brief explanation of what they came up.

From their graph they should be able to see that the graph they get it is a line.
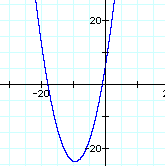
From their second exploration of multiplying two different linear functions they should see that by multiplying two linear functions will give you a parabola.
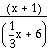
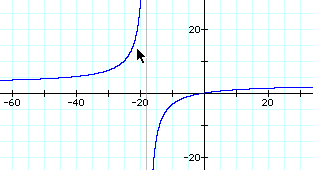
By dividing two different linear functions they should be able to tell that the graph is a hyperbola.
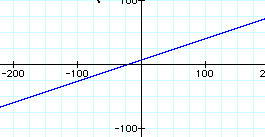
Finally, from their last exploration they should see that they get another line as in part i.
I would make them do at least three different examples of different pairs of linear functions to make sure that they can back up their results.
The second step they will be asked to do is use a different f(x) and g(x) from their first exploration, but at the same time they need to be the same.
f(x)= x and g(x)=x
They should follow all of the steps as above and write a brief statement of what type of graph they get and explain whether or not they got the same results as in the first exploration.
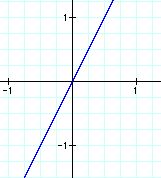
From this graph they should see that they got a graph of a line as in the first set of explorations.
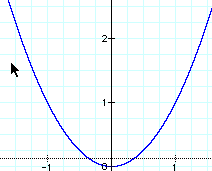
They should see that their graph looks like the same as in the first example part ii. That would be because when we multiply two linear functions together we receive a function with degree two. This is because when we multiply we add exponents and two x's of degree one multiplied give us degree two.
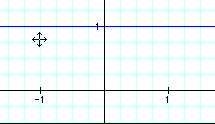
They should see that their result in this case is different from their previous exploration in example one. In example one when we divided we got a graph of a hyperbola. In this exploration when the two functions are the same we will get the line y=1. That is because anything function over itself gives us one.
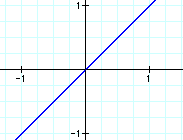
This looks the same as the picture in step one of example two, the only only difference is the slope. In the first step, the slope is 2 and the fourth step the slope is 1.
I would again ask my students to do a few more examples where there f(x) and g(x) are equal to see the similarities clearly.
The third step in their exploration is to look at f(x) and g(x) that are inverses to each other.
For example 3:
f(x) = x and g(x)= -x
As mentioned in the previous explorations, the students should show all steps and briefly write their comparisons to the other explorations.
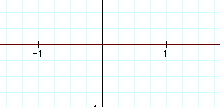
It is difficult to see, but the graph is the line y=0. Therefore, as in the above explorations the students should see that when you add two linear functions you get a line.
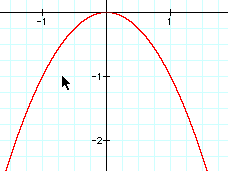
Hopefully the students would see that as in the previous examples that when you multiply two linear equations they will get a parabola.
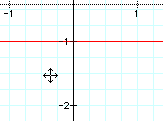
From this example, the students should see that it follows from example two. When they divide two linear equations, as long as they are not equal, that you will get a line.
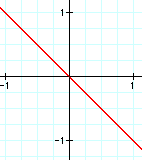
From this last step, the students should see that just like all the previous examples when they do the composition of the linear functions they get a line. I would also have them give a few more examples of this.
Therefore, this would be an excellent way to allow your students to explore with linear functions. It gives them a fun way to explore with the different software programs available to make math fun. This definitely is the perfect way to integrate technology into your mathematics instruction.