
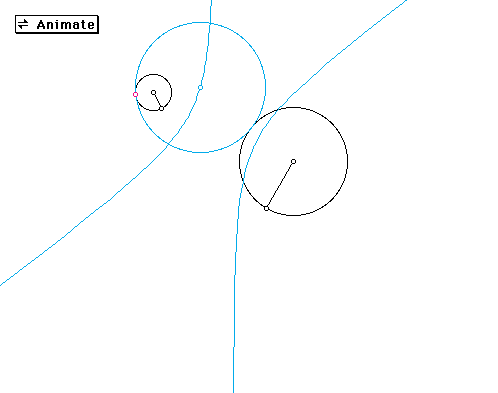
First, I constructed the tangent circle to two given circles if the given point is on the smaller of the two circles so that the smaller circle is external to the second circle.

The blue circle is the constructed circle tangent to both circles through a given point (pink).
Next I traced the center of the constructed tangent circle as the given point is rotated around the circle.
The absolute value of the difference of the segments from the center of the constructed circle to the centers of the two given circles is constant. The locus of the centers of the tangent circles is a hyperbola with foci at the center of the given circles.
A rough sketch of the result is below:
When the smaller circle is internal to the tangent circle the loci of the centers do not form a hyperbola.
Construct the tangent circle to two given circles if the given point is on the smaller of the two circles and the smaller circle is internal to the other circle.
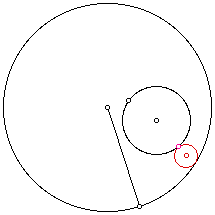
The red circle is the constructed circle tangent to both given circles through the given point (pink) on the smaller circle.
Next I traced the center of the constructed tangent circle as the given point is rotated around the circle.
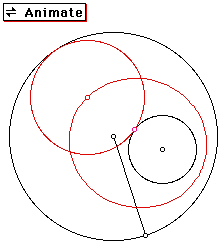
The sum of the segments from the center of the constructed circle to the centers of the two given circles is constant. The locus of the centers of the tangent circles is an ellipse with foci at the center of the given circles.
A rough sketch of the ellipse is below:
Return to home page.