Write-up #9
Pedal Triangles
by Beverly Hales and Mark Cowart
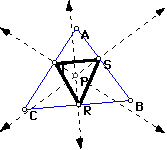
Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC through P with three points R, S, and T that are the intersections of the sides of the Triangle ABC. Triangle RST is the Pedal Triangle for Pedal Point P.

A pedal triangle can be made with any triangle and a given points. Click pedal for script.
I tried placing the pedal point as a point associated with triangles and then rotating one of the vertices of the the original triangle around the circumcircle of the triangle.
The most interesting observation occurred with the cirmcumcenter as the pedal point. By tracing the sides of the pedal triangle while rotating a vertex of the original triangle about the circumcircle a cylinder is formed, whereas one side forms the lateral side while the other two sides form the circular bases.
The Simson Line is the formed by the three vertices of the Pedal triangle being collinear. This occurs when the pedal point of the triangle lies on the circumcircle.
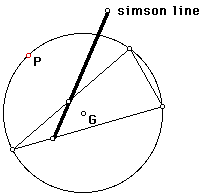
Find the envelope of the Simson line as the Pedal point is moved along the circumcircle.
By tracing the line, we find that the Simson line is collinear with each side of the triangle as the pedal point is collinear with the diameter of the circle containing the opposite vertex of the triangle.
Return to Home Page