ESSAY # 1
ROOTS TO EQUATIONS
by
Mark Cowart
The purpose of this essay is to demonstrate some explorations of finding roots to an equation using Algebra Xpressor, the Geometers Sketchpad, and the Excel software program. The solution to a given equation will be shown using a graphing technique, a spreadsheet graph, and an iteration process that demonstrates a convergence or divergence towards or away from the given equation's roots.
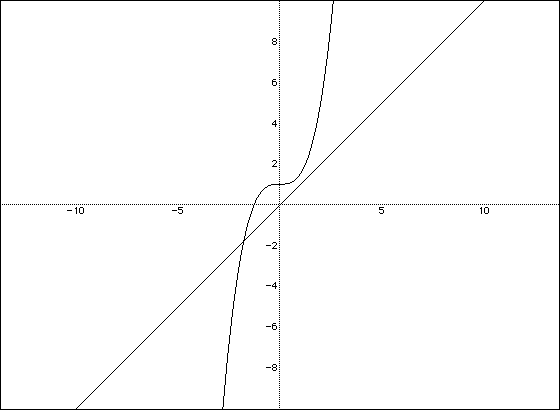
The equation demonstrated will be x^3 - 2x + 2 = 0. Solving the equation for x yields x = (x^3 + 2)/2. By substituting y = x, the intersection of the equation y = (x^3 + 2)/2 with the y = x line can be examined to see, in this case, the one solution of the original equation.

Next, the solution can be examined using a spreadsheet on Excel. The original value picked for A1 helps determine how quickly the graph may converge to a solution or diverge away from the curve. From the spreadsheet, Excel has the option to graph the inputs for A1 which allow for a visual inspection of the validity of the possible solution. The choices for the solution to the equation can be fine-tuned in such a way as to get a solution that is accurate to the nearest hundredth or better. This process is similar to students "zooming" in on the graph on the TI81, TI83, or TI85 graphing calculators. It is also a process of iteration, since values picked as a solution are created and examined to see where the function value of y will finally approach zero. The picture below shows an Excel spreadsheet graph where the solution to the original equation y = (x^3 + 2)/2 has an approximate solution of -1.26.
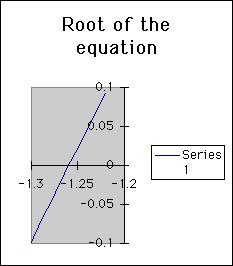
Students can see how the spreadsheet demonstrates that the input for x at -1.25 gives .0234325 and the x-value of -1.26 gives -.000188. Obviously, the only solution to the original equation is between these values, -1.25 and -1.26. Furthermore, values other than the solution will quickly diverge towards very large numbers. This can be visually shown using a GSP sketch.
A GSP sketch, with the Algebra Xpressor graph of the original equation pasted onto the sketch will allow iteration to be shown by drawing segments from the x-axis to the graph of the curve. Once again, this serves the purpose of showing the roots of the equation and where a convergence to a root may occur. Also, divergence away from the roots based on the choice from the x-axis can be observed.
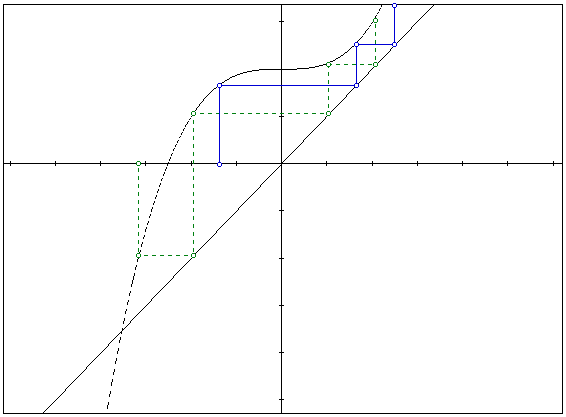
In the GSP sketch above, the blue and green segments go away from the only solution of the equation. The iteration of segments does not give a convergence. A student could see the geometric connection between the choices for a solution and the graph of the curve.
Now that the root(s) to a particular equation have been explored using the three software packages, students could use the same approaches to find roots to other equations. It could be an interesting way to tie together, in a concrete fashion, the ideas of statistics, graphing, and geometry to make mathematics more interesting, useful, and meaningful.