ESSAY #2
THE THEOREM OF THE BROKEN CHORD
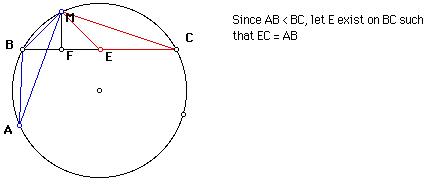
The Arabian scholar Abu'l Raihan al'biruni has attributed to Archimedes the theorem of the broken chord, which asserts that if, as shown in the GSP sketch to follow, AB and BC make up a broken chord in a circle, where BC > AB, and if M is the midpoint of arc ABC, then the foot F of the perpendicular from M on BC is the midpoint of the broken chord ABC.
Illustrations of this theorem can be explored using GSP which show that AB + BF = FC. Click here for a sketch.
The proof of this theorem can be done by using congruent triangles and their congruent parts to create an isosceles triangle with point F as the midpoint of its base. (refer to sketch below)

From the given we know AM = CM since chords inscribed in congruent arcs are congruent. Also, the measure of angle A = measure of angle C since both are inscribed angles intersecting chord BM. With EC = AB, as stated in the figure, there is a Side-Angle-Side congruence between triangle ABM and triangle CEM. This makes corresponding parts BM and ME congruent, which proves that triangle MBE is isosceles. If the isosceles triangle has MF as its altitude, then it follows that triangle BMF and triangle EMF are congruent by the Hypotenuse-Leg Theorem. This allows for the necessary conclusion that BF = FE. With AB = EC and BF = FE, addition yields the desired result of AB + BF = FE + EC. And since FE + EC = FC, it follows that AB + BF = FC, proving that the foot of the perpendicular F is the midpoint of the broken chord ABC.
Uses of this theorem in a high school geometry class include the following:
* allows students to use congruent triangle proofs they have practiced/mastered to prove a higher theory
* students develop concepts of congruent chords, inscribed angles, and congruent arcs
* allows for use of the GSP software to demonstrate and explore the theorem
* provides opportunity to develop the history of mathematics and Archimedes' contributions