Problem: Given a 3 x 3 x 3 cube made up of 27 1x1 blocks, If the cube is painted a given block may have 0, 1, 2, or 3 of its faces painted. count how many of each.
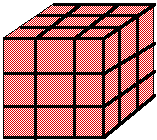
In the cube above we can visuatlize taking it apart. We begin counting the blocks that have 3 sides painted. Looking at this we know that the corners of the cube are the only blocks that have three sides painted and there are eight of them.
If we think of the cube as having three layers we notice that there are 4 blocks on each layer (top , bottom and middle) that have 2 faces painted giving us a total of twelve.
Next we count the number of 1 face painted. We know that the center block of each face of the cube has only one side painted. Since the cube has six faces, we conclude that there are six blocks with one face painted.
Finally, we can count the number of blocks with o faces painted. We find that the block in the very center, which is located in the middle of the second level is the only block that has no faces painted.
In summary, We have:
3 painted faces =8
2 painted faces = 12
1 painted face = 6
0 painted faces = 1
What about a 4 x 4 x 4?
Using similar reasoning from before we find that we have:
3 painted faces = 8
2 painted faces = 24
1 painted face = 24
0 painted faces = 8
Try a 5 x 5 x5. Do you see a pattern?
To generalize our findings for any cube of size n x n x n we know several things.
First, we know that the number of blocks with 3 sides painted will always be 8 because these blocks are the corners of our cube, No matter how large the cube it will always have only eight corners.
Second, we can find the number of cubes with two face painted by applying the formula:
(n-2)(4)(3) We get this from having four of thest blocks on each face and 3 on each level.
Third, we have the formula 
is the number of blocks with
one side painted.
Finally, we have 
is the blocks with zero sides painted.
A further observation is that we have a binomial cube