
Polar Equations
by Jamila K. Eagles
This assignment is an exploration of the polar equation:
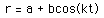
The special case of the equation occurs when a=b. It is often known
as the n-leaf rose. We begin our exploration with the question, What happen
to the graph as k varies? Let's take a look at the figure below.
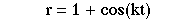
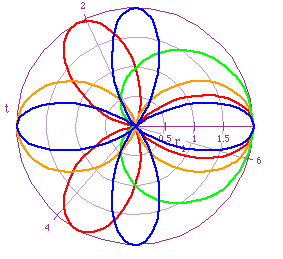
From the figure above , we can conclude that k determines the number
of "leaves" on our rose curve.
Our next investigation describes what happens when (a=b)
varies in the equation.
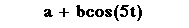

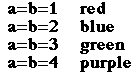
From the graph above, we can conclude that (a=b) determines the length
of each leaf on the rose curve. In each case, the length of the leaf is
2a. When a=1, the length is 2; a=3, the length is 6, .....
Now we want to take a look at the graph of r = bcos(kt). We will begin by
varying k. In the figure below, we have graphs of r=2cos(kt) as k goes from
2-5 respectively.
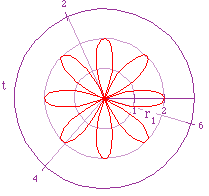
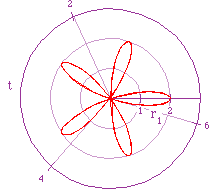
Notice that when k=2 the graph shows 4 leaves, and when k=3 the graph
shows 3 leaves. What type of pattern did you find? Looking further, we see
that when k=4 we have 8 leaves and when k=5 we have 5 leaves. We can conclude
that when k is even, the number of leaves is equal to 2k and when k is odd
, the number of leaves is equal to k.
Using the same graph bcos(5t) we want to see how changing b changes the
graph.
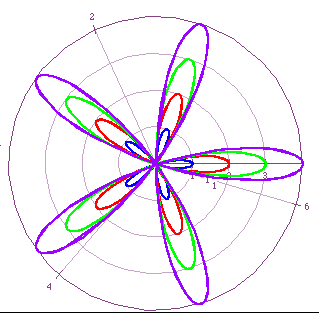
We notice that changing b, changes the length of the leaves. The length
in each case is equal to b.
Pulling together our findings up to this point we can compare the graphs
of a + bcos(kt) and bcos(kt), where a and b are equal.

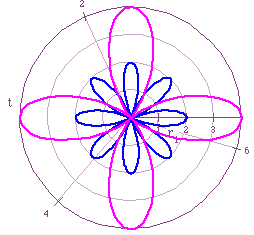
In Figure 1, we notice that the number of leaves are the same for each
graph. The number of leaves for the graph of r=bcos(kt) is equal to k since
k is odd. The graph of r=a+bcos(kt) always result in a graph with k leaves.
The difference comes in when talking about the length of each leaf. We noted
before that when r=bcos(kt) the length of each leaf is equal to b, and when
r=a+bcos(kt) the length of each leaf is equal to 2a(or 2b since a=b). In
summary, when k is odd the graphs of r = bcos(kt) have graphs with an equal
number of leaves, namely k and the length of the leaves of r = a +bcos(kt)
is twice the length of the leaves of r = a + bcos(kt).
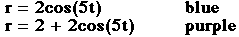
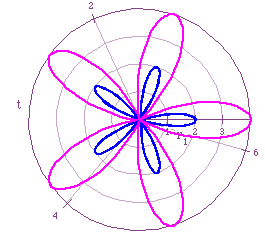
In Figure 2, we notice that the number of leaves on the graph of r=bcos(kt)
is twice the number of leaves on the graph of a + bcos(kt). Since k is odd,
the graph of r=bcos(kt) has 2k leaves. The lengths of the leaves follow
the same conclusion as in figure 1.
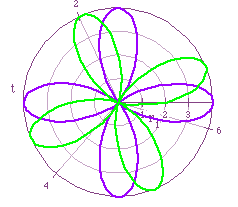
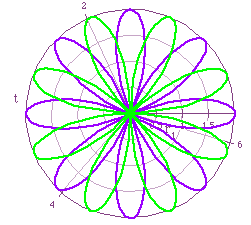
Finally we want to see what what happens to graphs when we replace cos
with sin. In the figures below we find that when we replace the cosine function
with the sine function in the two equations we get a slight shift in the
counter-clockwise direction. Knowing that sine and cosine are both periodic
funtions that have the same period and amplitude explains why the graphs
remain basically the same. Sine and cosine differ in position. When x =
0, sin(x)= 0 and cos(x)=1. This explains the change in position of the graphs.

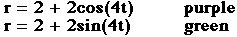


Our investigation of the n-leaf rose gives us an in-depth look at the different
parts of the equation and what effect they have on the curve.



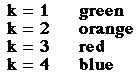

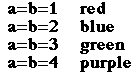





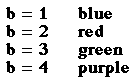

![]()

![]()

