---

It has now become a rather standard exercise, with available technology , to construct graphs to consider the equation:

and overlay several graphs of

for different values of a, b, or c as the other two are held constant. From these graphs discussion of the patterns for the roots of

can be followed. For example, if we set

for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.

We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ( In this equation (0,1)). From this graph, We can see the following:

When
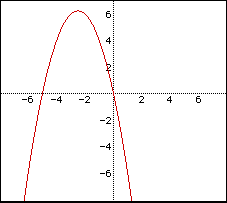
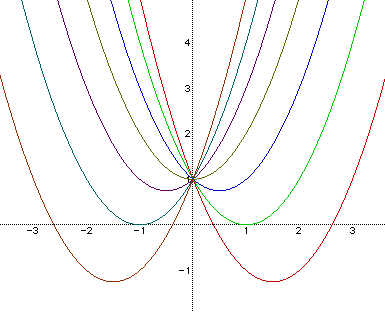
b < -2	2 real roots , both positive
b = -2	1 real root, positive
-1< b< 2	no real roots
b = 2	1 real root positive
b > 2	2 negative real roots

This can be determined by observing where the parabola intersects the x-axis for different values of b.


Another way to find the roots of the equation is to graph the relation in the xb plane.

We want to graph this relation in the xb plane. Meaning we solve the relation in terms of b. In this case we graph .

We get the following graph.

If we overlay this graph with b = -3, -2, -1, 0, 1, 2, and 3. We will have the following graph of horizontal lines.
 

Using this graph the roots can easily be found by simply looking at where the horizontal lines intersect the the graph of the relation.The roots are located at the actual point of intersection. In this case, we have:

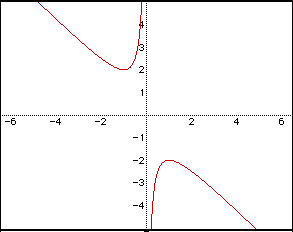
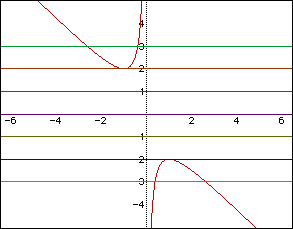
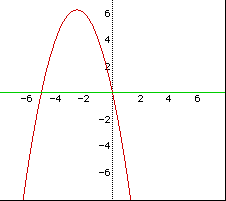
When
b > 2	2 negative real roots
b = 2	1 negative real root
-2 < b < 2	no real roots
b = -2	1 positive real root
b < -2	2 positive real roots

We find that this method gives us the same roots as the first method.

We can also find the roots by looking at the equation in terms of c. In the following example, we let b = 5 and consider the equation:

Graphing the equation in the xc plane, we first rewrite the equation by solving for c. We have and the graph looks like the following figure:

Looking at this graph we know that any value of c will be a horizontal line crossing the parabola in 0, 1, or 2 points and the roots being the value of c at the points of intersection. Using Algebra Expressor we can zoom in on the vertex and find that the value of c at the vertex is approximately 6.25. So we know that for c>6.25 the graph has no real roots, and for c=6.25 The equation has one real root, namely 6.25. If we overlay the graph with c = 0 we get the following graph:

We can conclude that when c< 6.25 The equation will have two real roots. Specifically, when 6.25<c<0 the roots will be negative, when c=0 one root will be negative and one root will be zero, and When c< 0 one root will be negative and the other positive.

The concept of finding roots of equations is traditionally taught by using the xy plane. Graphing the equation in different planes, xa, xb, ac, may give sudents a better understanding of the concept or give students an alternative approach to different problems.

Return to Write Ups

Return to Jamila's Page