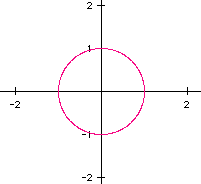
Some of the most interesting parametric curves are those involving the sine and cosine functions. This exploration will be done with the simplest of those, variations on x=cos(t) and y=sin(t).
We'll start with these equations as they stand and investigate variations. Let's check equations where t varies from 0 to 2 pi.

These basic parametric equations graph as a circle with radius 1. Let's see what happens if the coefficient of the sine and cosine are different. First we'll try 2 and 3 to see what happens when the coefficients are greater, and then we'll look at 1/2 and 1/4 to see what occurs when they are smaller.
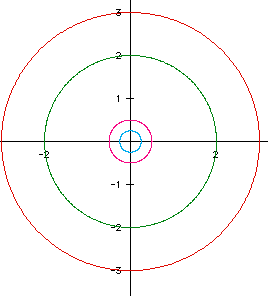
Not too surprisingly, there are four circles each with the radius of the coefficient we used in the equations. Let's check for negative coefficients. What happens if x=-2 cos(t) and y=-2 sin(t)? Let's also look at a negative fractional coefficient, say -1/2.
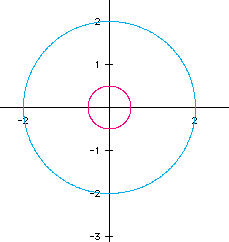
The only difference here appears to be that x-function prints the graph in a different color! When we think about the amplitude of the sin and cosine functions and how their graphs look on the xy-axis, it is not surprising that negative coefficients give the same graph here as positive ones.
Next let's look at graphs in which the coefficient of the sine function is different from the cosine function. What about x=2 cos(t) and y=1 sin (t)?
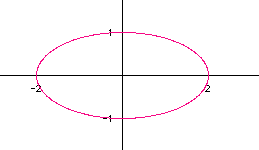
Now we have an ellipse whose major axis corresponds to the coefficient of the cosine function and whose minor axis corresponds to the coefficient of the sine function. Let's try a couple more examples of this type just to be sure. What about 3/4 and 3 for the cosine and 1/4 and 2 for the sine respectively?
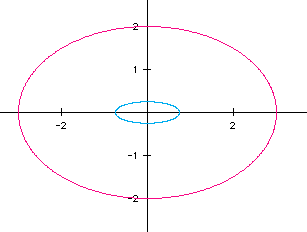
Just as expected! The cosine coefficient is doubled along the x-axis, and the sine coefficient is doubled along the y-axis. Okay, now let's try it with the the sine coefficient greater than the cosine one. Let graph y=2 cos (t) and x=3 sin (t). Also, on the same axes, let's graph y=1/2 cos(t) and x=3/2 sin(t).
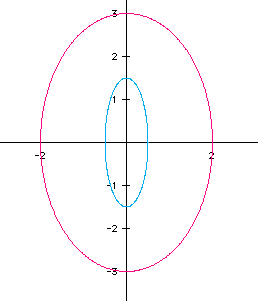
This time the ellipses are situated in the vertical direction. Can you explain why? Just for fun let's look at some equations with a mixture of the above conditions. How about this?
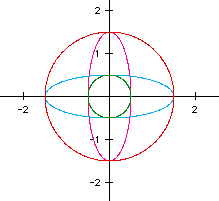
There are four sets of parametric equations graphed here. Can you figure out their equations? Look back at the above situations if you need to. Try graphing some parametric equations of your own. See if you can make some interesting designs.
Thre variations of graphing parametric equations are endless. Try some of the following:
1. x=cos(at) and y=sin(at) for different values of a and b.
2. x=a cos (t) + h sin(t) and y=b sin(t) + h cos(t) for different values of h.
3. x=a (cos(t))^2 and y=b(sin(t))^2 .