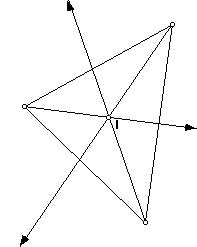
Let's construct a triangle and bisect each angle.

Notice that all three angle bisectors intersect in the same point. This is the incenter and is labeled I. When any two lines intersect they are said to be concurrent. Any two lines not parallel will have a point of concurrency, but it is special for three lines to meet in the same point. In this triangle, the point is the same distance from each side; so it is the center of a circle that can be inscribed in the triangle.A radius is formed by constructing a perpendicular to one side. The circle touches all three sides, but does not extend outside them.
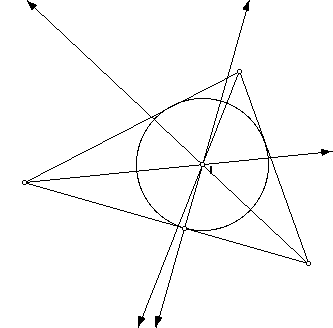
Investigate: What happens if the triangle is an obtuse one? What if it is a right triangle?
Make a conjecture about the incenters of various shapes of triangles.
Constuct another triangle and the altitudes which are perpendicular lines from the vertex to the line of the opposite side.
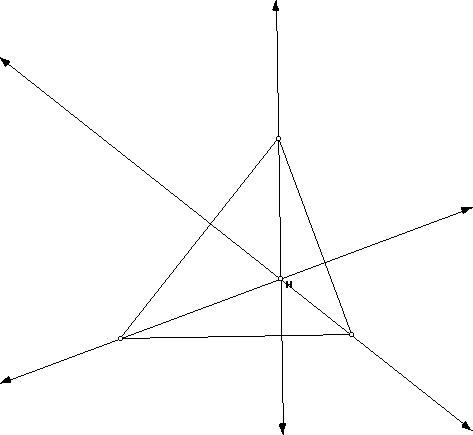
Notice again that the three lines intersect in the same point. This is called the orthocenter and is usually labeled H. Try this with an obtuse
Investigate: What happens if the triangle is obtuse? Hint: the sides of the triangle may need to be extended. What if it is a right triangle?
Make a conjecture about the orthocenters of the various shapes of triangles.
Draw another triangle and construct the three medians, the segments from each vertex to the middle of the opposite side.
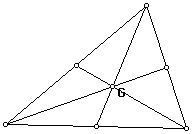
Again the three constructed lines intersect or concurr; the point of intersection is called the centroid and is labeled G. It divides each median into two parts so that the distance from the centroid to the vertex is two-thirds the distance from the centroid to the midpoint.
Investigate: What happens in obtuse triangles? What about right triangles? Make a conjecture about the centroids of triangles.
There is one more type of triangle center to explore. Construct the perpendicular bisectors of each side of a triangle.
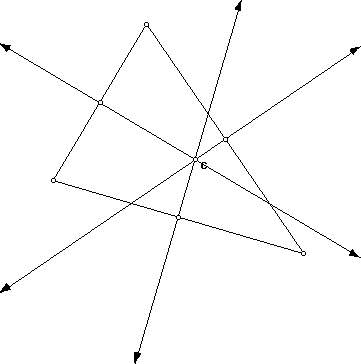
Once more the constucted lines intersect at a point; it is called the circumcenter and is labeled C. The circumcenter is the center of a circle which is circumscribed about the triangle. It touches each vertex of the triangle; a radius is a segment from the circumcenter to a vertex. Notice below.
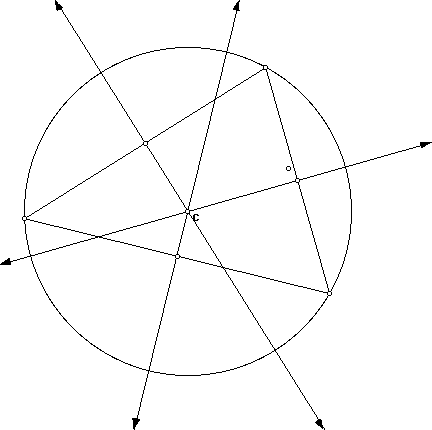
Investigate the circumcenter of obtuse triangles and right triangles. Make a conjecture about the circumcenters of various shapes of triangles.