Given a rectangular sheet of cardboard 15 in by 25 in. A small square of the same size is cut from each corner and each side folded up along the cuts to form a lidless box. What is the maximum volume of the box? The problem will be investigated using Algebra Xpresser, GSP, and Excel.
To find the volume of the box the length is multiplied by the width to get the area of the bottom which is then multiplied by the height. The height is what we don't know here, and as soon as a corner is cut out the width and length are changed. Let's write the equation this way using x for the side of the cut-out corner. Note that the corner cut out cannot be any larger than 7.5 inches.

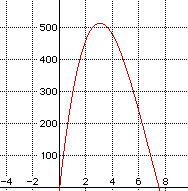
The x-axis on this graph represents the inches of the corner cut out; the y-axis is the cubic inches which are the volume of the box. The maximum volume appears to be a little more than 500 cubic inches. Let's look at that a little closer.
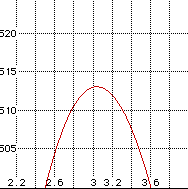
Now we see that the maximum is about 513 cubic inches and that value is attained when the corner cut out is just a little more than 3 inches. Let's look a little closer still.
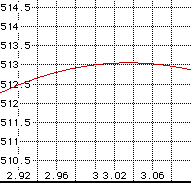
The maximum volume of the box is just over 513 cubic inches and the corner to be cut out is about 3.04 inches. Now it will be hard to cut cardboard any more accurately than that.
Now we need to find the depth of the cut which will produce a box with volume 400 cubic inches.We'll show the part of the graph close to 400.
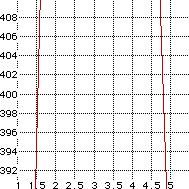
To make a volume of 400 cu. inches, the cut must be at 1.5 inches or at 4.8 inches. Either size square will produce the desired box.
Geometer Sketch Pad is not large enough to accomodate the measurements of 25 inches by 15 inches. This sketch is drawn to one-tenth scale. Using the GSP file and dragging point U or animating the sketch show the different volumes as the size of the cut changes. The greatest volume for this sketch is .513 cubic inches when the cut is .305 inches. The volume of 400 cubic inches in the original problem will show as .400 cubic inches in this sketch. This volume is attained when the cut is .153 and also at .476 inches, which corresponds to the 1.53 and the 4.76 inches found in Xpresser.
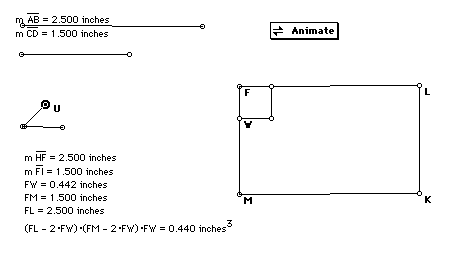
Click here to see and animate a GSP file.
A spreadsheeet is a convenient way to explore this box problem. Let x be the side of the square cut from each corner of the cardboard; this will be the height of the box after folding. Then 25-2x is the length of the cardboard after cutting, while 15-2x is the width. Multiplying length time width times height produces the volume of the box.
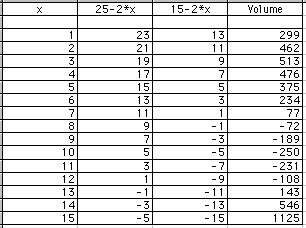
Notice that no cut larger than seven inches will work; this is expected since half the width of the box is seven and a half inches. The largest volume in this chart is 513 cubic inches when the cut is 3 inches. Let's check numbers close to 3 to get more accuracy.
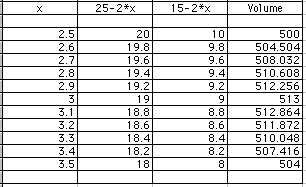
From this chart a cut of 3 inches gives the maximum volume. 3.1 is very close, so something between 3.0 and 3.1 would be more accurate, but this is sufficient for the purpose. Now we need to see what size cut is needed to give a box volume of 400 cubic inches. Notice from the first chart that 400 is between 1 and 2 and also between 4 and 5. So there are two possibilities. Let's try another chart first with numbers between 1 and 2.
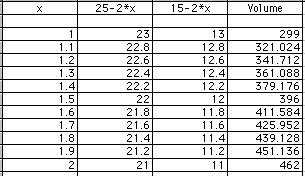
Now 396 is closest to 400 at 1.5 inches. Let's try numbers between 1.45 and 1.55 .
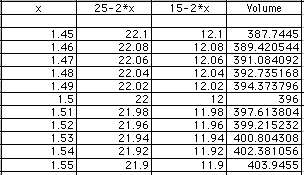
The number we want is between 1.52 and 1.53. This is accurate enough even if the cutting is done by machine. Now we'll look at the other possibility; it is when the cut is between 4 and 5 inches.
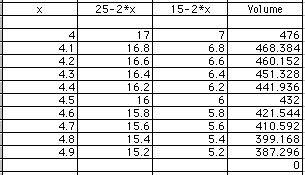
Now 400 is between 4.7 and 4.8, but closer to 4.8. We'll try two decimal places.
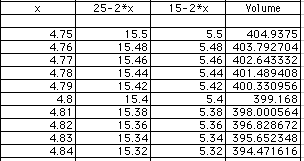
This is very close to 4.79 which is accurate enough for our purposes.
Of the three ways of finding the maximum volume and related problems, it seems that a spreadsheet is easier and quicker than either the algebra or geometry programs. But those give different and interesting perspectives.