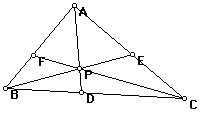
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections. Explore the (AF)(BD)(ED) and (FB)(DC)(EA) for various triangles and various locations of P.

The Theorem of Ceva follows from the Theorem of Meneluas.
The Theorem of Meneluas stated,
Given a Triangle ABC and points D on BC, E on CA and F on AB that do not coincide with the vertices of the triangle, the linearity number is determined by
When applying the Theorem of Menelus, the order of the points in the ratios are very important. The segment is viewed as a vector such that direction to and from the point are assigned positive and negative values.
Unlike lengths of segments, AB does not equal BA; instead, AB = -BA.
Using the linearity number to state the Theorem of Ceva is as follows:
Three lines are concurrent or parallel if [ABC/DEF] = 1.
There are two options to consider with the linearity number equal to 1. We can use an indirect proof by considering the possibility that the lines are parallel:
If D lies on BC, E lies on AC and F lies on AB, draw BC//AC//AB.
This is impossible by definition of parallel lines. Parallel lines are lines that do not intersect or share a common point. AC and AB share a common point at A, and BC and AC share a common point at C, and BC and AB share a common point at C.
The lines cannot be parallel, therefore, they are concurrent.
This theorem also applies if point p is outside the triangle. In order to show this relationship, I made the triangle using lines so that intersections would still occur even when the point was not in the interior of the triangle.
When P is inside the triangle, the ratios of the areas of the original triangle and the triangle formed the intersection points is always more than 4.
In order for the triangles to have a ratio
equal to 4, the interior triangle formed by the intersection point would
have to be 1/4 the size of the original triangle. This will occur when the
original triangle is equilateral and the point P is the centroid.
Return to Home Page